题目内容
 如图,设△ABC的面积是1,D是边BC上一点,且
如图,设△ABC的面积是1,D是边BC上一点,且 ,若在边AC上取一点,使四边形ABDE的面积为
,若在边AC上取一点,使四边形ABDE的面积为 ,则
,则 的值为________.
的值为________.

分析:首先连接AD,利用三角形的面积公式和边上的高相同,分别求出△ABD△ACD△ADE△CDE的面积,利用同高的三角形的面积比等于边之比即可求出答案.
解答:
 解:连接AD,设△ABD△ACD△ADE△CDE的面积分别为s1 s2 s3 s4,
解:连接AD,设△ABD△ACD△ADE△CDE的面积分别为s1 s2 s3 s4,∵△ABD的边BD上和△ACD的边CD上的高相同,
 =
= ,由面积公式得:
,由面积公式得: =
=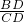 =
= ,
,∵△ABC的面积是1,
∴s1=
 ,s2=
,s2= ,
,∵四边形ABDE的面积为
 ,
,即s3+s1=
 ,
,∴s3=
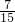 ,
,∴s4=s2-s3=
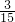 ,
,∵△AED的边AE上和△ECD的边CE上的高相同,由面积公式得:
 =
= =
= =
= .
.故答案为:
 .
.点评:本题主要考查了对三角形的面积公式的灵活运用和掌握,特别是对三角形等高时面积之比等于边之比的巧妙运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
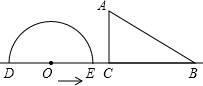

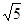 个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
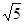 个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面
积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面
积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
