题目内容
方程组 有唯一解,求m的值和方程组的解?
有唯一解,求m的值和方程组的解?
【答案】分析:把方程组转化成一元二次方程,根据已知得出b2-4ac=0,求出m的值,代入方程组求出方程组的解即可.
解答:解: ,
,
∵由②得:y=x+m③,
把③代入①得:x2+(x+m)2-1=0,
即2x2+2mx+m2-1=0,④
∵方程组 有唯一解,
有唯一解,
∴△=(2m)2-4•2•(m2-1)=0,
m=± ,
,
当m= 时代入④得:2x2+2
时代入④得:2x2+2 x+1=0,
x+1=0,
解得:x1=x2=- ,
,
代入③得:y1=y2= ,
,
当m=- 时代入④得:2x2-2
时代入④得:2x2-2 x+1=0,
x+1=0,
解得:x3=x4= ,
,
代入③得:y3=y4=- ,
,
即m的值是 和-
和- ,方程组的解是:
,方程组的解是: ,
, .
.
点评:本题考查了解高次方程和一元二次方程的根的判别式的应用,关键是求出m的值.
解答:解:
 ,
,∵由②得:y=x+m③,
把③代入①得:x2+(x+m)2-1=0,
即2x2+2mx+m2-1=0,④
∵方程组
 有唯一解,
有唯一解,∴△=(2m)2-4•2•(m2-1)=0,
m=±
 ,
,当m=
 时代入④得:2x2+2
时代入④得:2x2+2 x+1=0,
x+1=0,解得:x1=x2=-
 ,
,代入③得:y1=y2=
 ,
,当m=-
 时代入④得:2x2-2
时代入④得:2x2-2 x+1=0,
x+1=0,解得:x3=x4=
 ,
,代入③得:y3=y4=-
 ,
,即m的值是
 和-
和- ,方程组的解是:
,方程组的解是: ,
, .
.点评:本题考查了解高次方程和一元二次方程的根的判别式的应用,关键是求出m的值.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 有唯一解,求m的值和方程组的解?
有唯一解,求m的值和方程组的解?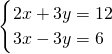 的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组
的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组 =4-
=4- x
x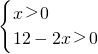 则有0<x<6
则有0<x<6
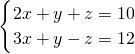 的正整数解.
的正整数解.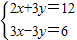 的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组
的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组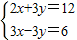 有唯一解.
有唯一解.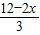 =4-
=4- x
x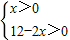 则有0<x<6
则有0<x<6 x为正整数,则
x为正整数,则 x为正整数,所以x为3的倍数.
x为正整数,所以x为3的倍数. ×3=2
×3=2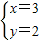
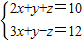 的正整数解.
的正整数解.