Question

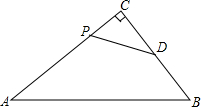如图，Rt△ABC中，∠C=90°，AC=8，BC=6，点D是BC边的中点，动点P从点C出发，沿C→A→B的方向在AC、AB边上以每秒2个单位的速度向点B移动，运动至点B即停止．连接PD，当点P运动时间t=________时，线段PD截Rt△ABC为两部分所得的三角形与Rt△ABC相似．

Answer 1

或2或或8.1
分析：此题可转化为过点D的直线，截△ABC，使截得的三角形与△ABC相似，又题意可知有四条，即线段PD截Rt△ABC为两部分所得的三角形与Rt△ABC相似有四种情况，分别求出此时的t即可．
解答：①当△CPD∽△CAB时；t=；
②当△CPD∽△CBA时；t=2；
③当△DPB∽△CAB时；t=；
③当时△PBD∽△CBA时；t=8.1．
故答案为：或2或或8.1．
点评：本题主要考查相似三角形性质的运用，在解答问应分四种情况进行求解，在解题过程应防止漏解或错解．