题目内容
用适当的方法解下列方程:
(1)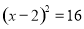 (2)
(2)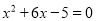
在数轴上实数a,b的位置如上图所示,化简|a+b|+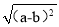 的结果是( )
的结果是( )
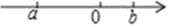
A. ﹣2a﹣b B. ﹣2a+b C. ﹣2b D. ﹣2a
D 【解析】如图所示:可得,a+b<0,a?b<0, 故原式=?(a+b)?(a?b)=?2a. 故选:D.若分式方程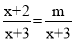 无解,则m的值为( )
无解,则m的值为( )
A. ﹣1 B. 0 C. 1 D. 3
查看答案已知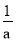 ﹣
﹣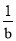 =
=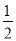 ,则
,则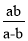 的值为( )
的值为( )
A. 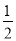 B.
B. 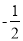 C. ﹣2 D. 2
C. ﹣2 D. 2
如图,AB=AD,要说明△ABC≌△ADE,需添加的条件不能是( )
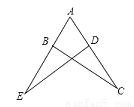
A. ∠E=∠C B. AC=AE C. ∠ADE=∠ABC D. DE=BC
查看答案如图,从边长为a的正方形中去掉一个边长为b的小正方形,然后将剩余部分剪开后拼成一个长方形,上述操作能验证的等式是( )
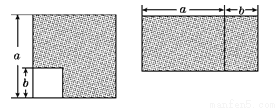
A. (a+b)(a-b)=a2-b2 B. (a-b)2=a2-2ab+b2
C. (a+b)2=a2+2ab+b2 D. a2+ab=a(a+b)
查看答案如果分式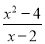 的值等于0,那么( )
的值等于0,那么( )
A. 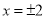 B.
B. 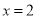 C.
C. 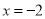 D.
D. 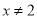
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
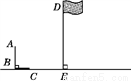
如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
解方程:x+5=x2-25.
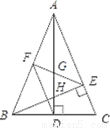
查看答案如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=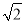 AE2;④S△ABC=4S△ADF.其中正确的有___________.
AE2;④S△ABC=4S△ADF.其中正确的有___________.
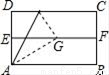
如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=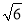 ,AD=2.当AB=_______时,△ABC与△ACD相似.
,AD=2.当AB=_______时,△ABC与△ACD相似.
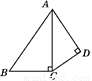
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 _______
设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


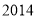 ,
, 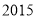 ,
, 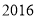 ,
, 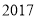 这四个数中,不能表示为两个整数平方差的数是( ).
这四个数中,不能表示为两个整数平方差的数是( ).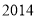 B.
B. 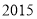 C.
C. 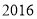 D.
D. 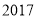
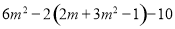 ,其中
,其中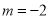 .
.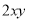 是同类项的是( )
是同类项的是( )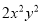 B.
B. 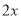 C.
C. 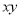 D.
D. 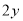
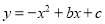 经过点A(3,0),B(﹣1,0).
经过点A(3,0),B(﹣1,0).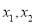 是一元二次方程
是一元二次方程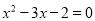 的两个根,则
的两个根,则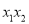 的值是( )
的值是( )