题目内容
已知:如图,菱形ABCD中,∠A=120°,过C分别作AB、AD的垂线,垂足分别为E、F,与对角线BD相交于G、H。
求证:(1)△GBC≌△HDC ;
(2)△CGH 是等边三角形。
求证:(1)△GBC≌△HDC ;
(2)△CGH 是等边三角形。
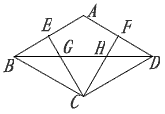
证明:(1)∵ABCD为菱形,∠A=120°,
∵∠B=∠D=60°
又∵CE⊥AB,CF⊥AD
∴∠BCG=∠HCD=30°
又∵BD是对角线
∴∠CBG=∠HDC=30°
BC=DC
∴△GBC≌△HDC
(2)∵CG=CH
∴∠GCH=60°
∴△GCH为等边三角形
∵∠B=∠D=60°
又∵CE⊥AB,CF⊥AD
∴∠BCG=∠HCD=30°
又∵BD是对角线
∴∠CBG=∠HDC=30°
BC=DC
∴△GBC≌△HDC
(2)∵CG=CH
∴∠GCH=60°
∴△GCH为等边三角形

练习册系列答案
相关题目
 17、已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为
17、已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为
 22、已知:如图,菱形ABCD中,E、F分别是AB、AD上的点,且AE=AF.
22、已知:如图,菱形ABCD中,E、F分别是AB、AD上的点,且AE=AF.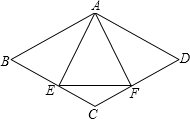 已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;
已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF; (2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.
(2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.