题目内容
10.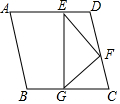 如图,点E、F分别是菱形ABCD边AD,CD的中点,EG⊥BC于点G,∠GEF=50°,则∠A的度数是( )
如图,点E、F分别是菱形ABCD边AD,CD的中点,EG⊥BC于点G,∠GEF=50°,则∠A的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
分析 如图,延长GF交AD的延长线于M.由△FDM≌△FCG,FM=FG,利用直角三角形斜边中线的性质,可得EF=FM=GF,再求出∠M,证明DF=DM,即可求出∠FDM,延长即可解决问题.
解答 解:如图,延长GF交AD的延长线于M.
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠M=∠CGF,
在△FDM和△FCG中,
$\left\{\begin{array}{l}{∠M=∠FGC}\\{∠DFM=∠CFG}\\{DF=CF}\end{array}\right.$,
∴△FDM≌△FCG,
∴FM=FG,
∵EG⊥CB,AD∥CB,
∴EG⊥AD,
∴∠GEM=90°,
∴EF=FM=FG,
∴∠M=∠FEM,
∵∠GEF=50°,
∴∠M=50°,
∵CG=CF,CG=DM,
∴DF=DM,
∴∠M=∠DFM=50°,
∴∠FDM=180°-50°-50°=80°,
∵AB∥CD,
∴∠A=∠CDM=80°.
点评 本题考查了菱形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,作辅助线构造出全等三角形和直角三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
20.已知$\sqrt{a-1}$+(b+2)2=0,则(a+b)2017的值为( )
| A. | 0 | B. | 2016 | C. | -1 | D. | 1 |
1.已知点A(2,-3),如果点A关于x轴的对称点是B,那么B点的坐标是( )
| A. | (-3,2) | B. | (-2,-3) | C. | (2,3) | D. | (-2,3) |
5.下列二次根式与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{2\frac{1}{2}}$ | B. | $\sqrt{\frac{2}{5}}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{\frac{4}{5}}$ |
15.下列二次根式中是最简二次根式的是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{8}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{20}$ |
19.将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,则这个扇形圆心角的度数为( )
| A. | 30°,60°,90° | B. | 60°,120°,180° | C. | 50°,100°,150° | D. | 80°,120°,160° |
 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是48,则DP的长是4$\sqrt{3}$.
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是48,则DP的长是4$\sqrt{3}$.