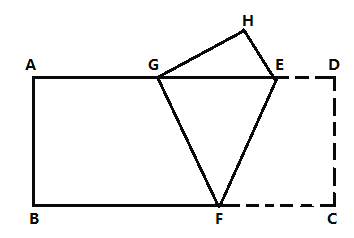
题目内容
【题目】如图，在长方形纸片
中，
，
，拆叠纸片，使顶点
落在边
上的点
处，折痕分别交边、
于点
、
,则
的面积最大值是__________．
【答案】7.5
【解析】
当点G与点A重合时，
面积最大，根据折叠的性质可得GF=FC，∠AFE=∠EFC，根据勾股定理可求出AF=5，再根据矩形的性质得出∠EFC=∠AEF=∠AFE，可得AE=AF=5，即可求出△GEF的面积最大值．
解：如下图，当点G与点A重合时，面积最大，
由折叠的性质可知，GF=FC，∠AFE=∠EFC，
在Rt△ABF中，
，
∴
解得：AF=5，
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠AEF=∠CFE，
∴∠AEF=∠AFE
∴AE=AF=5，
∴△GEF的面积最大值为：
，
故答案为：7.5．
练习册系列答案
相关题目
【题目】我区浙江中国花木城组织10辆汽车装运完A、B、C三种不同品质的苗木共100吨到外地销售，按计划10辆汽车都要装满，且每辆汽车只能装同一种苗木，由信息解答以下问题：
苗 木 品 种 | A | B | C |
每辆汽车运载量（吨） | 12 | 10 | 8 |
每吨苗木获利（万元） | 3 | 4 | 2 |
（1）设装A种苗木车辆数为x，装运B种苗木的车辆数为y，求y与x之间的函数关系式；
（2）若装运每种苗木的车辆都不少于2辆，则车辆安排方案有几种？写出每种安排方案
（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润．
