题目内容
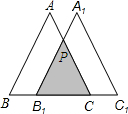 如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3,
如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3,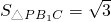 ,则BB1=________.
,则BB1=________.
1
分析:过P作PD⊥B1C于D,根据等边三角形和平移性质得出∠PB1C=∠C=60°,求出△PCB1是等边三角形,设等边三角形PCB1的边长是2a,得出B1D=CD=a,由勾股定理求出PD,根据三角形的面积公式得出 ×2a×
×2a× a=
a= ,求出a即可.
,求出a即可.
解答:过P作PD⊥B1C于D,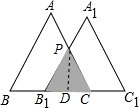
∵将等边△ABC沿BC方向平移得到△A1B1C1,
∴∠PB1C=∠C=60°,
∴∠CPB1=60°,
∴△PCB1是等边三角形,
设等边三角形PCB1的边长是2a,
则B1D=CD=a,
由勾股定理得:PD= a,
a,
∵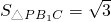 ,
,
∴ ×2a×
×2a× a=
a= ,
,
解得:a=1,
∴B1C=2,
∴BB1=3-2=1.
故答案为:1.
点评:本题考查了等边三角形的性质,平移的性质,勾股定理,三角形的面积的应用,解此题的关键是得出关于a的方程,题目比较典型,是一道比较好的题目.
分析:过P作PD⊥B1C于D,根据等边三角形和平移性质得出∠PB1C=∠C=60°,求出△PCB1是等边三角形,设等边三角形PCB1的边长是2a,得出B1D=CD=a,由勾股定理求出PD,根据三角形的面积公式得出
 ×2a×
×2a× a=
a= ,求出a即可.
,求出a即可.解答:过P作PD⊥B1C于D,

∵将等边△ABC沿BC方向平移得到△A1B1C1,
∴∠PB1C=∠C=60°,
∴∠CPB1=60°,
∴△PCB1是等边三角形,
设等边三角形PCB1的边长是2a,
则B1D=CD=a,
由勾股定理得:PD=
 a,
a,∵
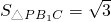 ,
,∴
 ×2a×
×2a× a=
a= ,
,解得:a=1,
∴B1C=2,
∴BB1=3-2=1.
故答案为:1.
点评:本题考查了等边三角形的性质,平移的性质,勾股定理,三角形的面积的应用,解此题的关键是得出关于a的方程,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
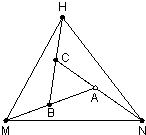 8、如图,将等边△ABC各边向外延伸一倍,构成一个新的△NMH,若△ABC的面积为1,则△NMH的面积是( )
8、如图,将等边△ABC各边向外延伸一倍,构成一个新的△NMH,若△ABC的面积为1,则△NMH的面积是( )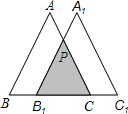 (2012•宁夏)如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3,
(2012•宁夏)如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3, 如图,将等边△ABC竖直向上平移到与BC的距离为2cm的△A′B′C′处,若AB=
如图,将等边△ABC竖直向上平移到与BC的距离为2cm的△A′B′C′处,若AB= 如图,将等边△ABC剪去一个角后,∠BDE+∠CED=
如图,将等边△ABC剪去一个角后,∠BDE+∠CED=