题目内容
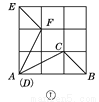
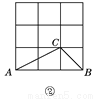
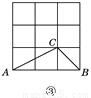
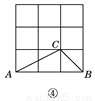
如图,在3×3的正方形网格中,格点△ABC和格点△DEF关于某条直线成轴对称,图①中已将△DEF画出,请你在图②,图③,图④中分别画出一个不同的、符合条件的△DEF.
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
题目内容
如图,在3×3的正方形网格中,格点△ABC和格点△DEF关于某条直线成轴对称,图①中已将△DEF画出,请你在图②,图③,图④中分别画出一个不同的、符合条件的△DEF.




 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案