题目内容
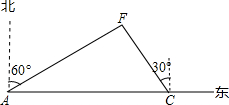一艘轮船自西向东航行，在A处测得北偏东60°方向有一座小岛F，继续向东航行80海里到达C处，测得小岛F此时在轮船的北偏西30°方向上．轮船在整个航行过程中，距离小岛F最近是多少海里？（结果保留根号）
分析：过点F作DF⊥AC，根据三角函数关系，用DF表示出AC，再由AC=80可得出DF的长度，也即最短距离．
解答：
解：过点F作DF⊥AC，垂足为D
在Rt△ADF中，∠FAD=30°，tan∠FAD=
∴AD=
=
DF，
在Rt△CDF中，∠FCD=60°，tan∠DCF=
∴CD=
=
DF
∵AC=AD+CD=80
∴
DF+
DF=80，解得：DF=20
（海里）
答：距离小岛F最近距离为20
海里．
解：过点F作DF⊥AC，垂足为D在Rt△ADF中，∠FAD=30°，tan∠FAD=
| DF |
| AD |
∴AD=
| DF |
| tan∠FAD |
| 3 |
在Rt△CDF中，∠FCD=60°，tan∠DCF=
| DF |
| CD |
∴CD=
| DF |
| tan∠DCF |
| ||
| 3 |
∵AC=AD+CD=80
∴
| 3 |
| ||
| 3 |
| 3 |
答：距离小岛F最近距离为20
| 3 |
点评：本题考查解直角三角形的应用，有一定难度，关键在于运用三角函数关系用DF表示出AC，最终求出DF的长度．
练习册系列答案
名校课堂系列答案
相关题目
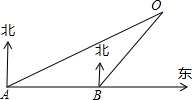如图所示，在海平面上灯塔O方圆100km范围内有暗礁，一艘轮船自西向东航行，在点A处测得灯塔O在北偏东60°方向上，继续航行100km后，在B处测得灯塔O在北偏东37°方向上，请你作出判断，为了避免触礁，这艘轮船
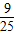，tan21.3°≈
，sin63.5°≈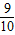
，tan63.5°≈2）