题目内容
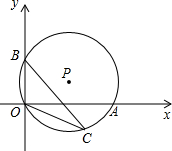如图，经过原点的⊙P与两坐标轴分别交于点A（2
，0）和点B（0，2），C是优弧
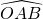上的任意一点（不与点O，B重合），则tan∠BCO的值为
- A.
- B.
- C.
- D.
A
分析：连结AB，根据正切的定义得到tan∠A=
=，再根据圆周角定理得∠C=∠A，所以tan∠BCO=．
解答：
解：连结AB，如图，
∵∠AOB=90°，
而A（2，0）和点B（0，2），
∴tan∠A==
=，
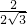∵∠C=∠A，
∴tan∠BCO=．
故选A．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
分析：连结AB，根据正切的定义得到tan∠A=
=，再根据圆周角定理得∠C=∠A，所以tan∠BCO=．解答：
解：连结AB，如图，∵∠AOB=90°，
而A（2
，0）和点B（0，2），∴tan∠A=
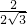==，∵∠C=∠A，
∴tan∠BCO=
．故选A．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．
练习册系列答案
阅读快车系列答案
相关题目
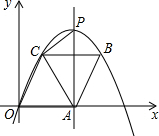、C在这条抛物线上，如果四边形OABC是菱形，
（2012•温州）如图，经过原点的抛物线y=-x2+2mx（m＞0）与x轴的另一个交点为A．过点P（1，m）作直线PM⊥x轴于点M，交抛物线于点B．记点B关于抛物线对称轴的对称点为C（B、C不重合）．连接CB，CP．
（2013•太原二模）如图，经过原点的抛物线y1=x2+2x与x轴交于点A，将它平移得到抛物线y2=（x-2）2+1．有以下结论：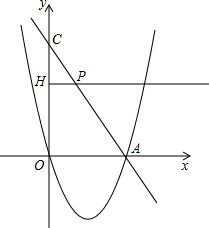
如图，经过原点的抛物线y=x2-2mx与x轴的另一个交点为A．过点P（m+1，