题目内容
如图,在平面直角坐标系xOy中,已知点B的坐标为(2,0),点C的坐标为(0,8),sin∠CAB= , E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.
, E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.

(1)求AC和OA的长;
(2)设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式;
(3)在(2)的条件下试说明S是否存在最大值,若存在,请求出S的最大值,并求出此 时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
(1)AC=10;OA=6;(2)S=-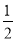
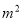 +4m;(3)E(-2,0);△BCE为等腰三角形.
+4m;(3)E(-2,0);△BCE为等腰三角形.
【解析】
试题分析:(1)根据点坐标求出OB和OC的长度,根据∠CAB的正弦值求出AC,根据△AOC的勾股定理求出OA;(3)根据相似求出EF与m的关系,根据∠EFG的正弦值求出FG与m的关系,然后根据S=△BCE的面积减去△BFE的面积进行计算;(3)根据二次函数的最值问题求出点E的坐标,然后进行判定.
试题解析:(1)∵点B的坐标为(2,0),点C的坐标为(0,8), ∴OB=2, OC=8.

在Rt△AOC中,sin∠CAB=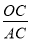 =
=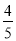 ∴
∴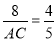 AC=10 ∴
AC=10 ∴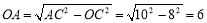
(2)依题意,AE=m,则BE=8-m. ∵EF∥AC,
∴△BEF∽△BAC. ∴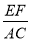 =
=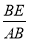 . 即
. 即 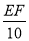 =
=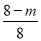 .
.
∴EF=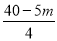 .
.
过点F作FG⊥AB,垂足为G. 则sin∠FEG=sin∠CAB=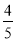 .
.
∴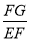 =
= . ∴FG=
. ∴FG=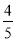
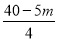 =8-m.
=8-m.
∴S=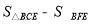 =
=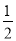 (8-m)×8-
(8-m)×8-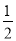 (8-m)(8-m)=-
(8-m)(8-m)=-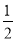
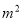 +4m.
+4m.
自变量m的取值范围是0<m<8.
(3) S存在最大值. ∵S=-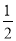
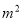 +4m=
+4m=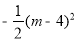 +8,且-
+8,且-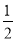 <0,
<0,
∴当m=4时,S有最大值,S最大值=8
∵m=4, ∴点E的坐标为(-2,0) ∴△BCE为等腰三角形.
考点:相似三角形的应用、二次函数的应用.

 阅读快车系列答案
阅读快车系列答案 的图象上有点P1,P2,P3,…,Pn,Pn+1,它们的横坐标依次为1,2,3,…,n,n+1.过点P1,P2,P3,…,Pn,Pn+1分别作x轴、y轴的垂线段,构成如图所示的若干个矩形,将图中阴影部分的面积从左至右依次记为
的图象上有点P1,P2,P3,…,Pn,Pn+1,它们的横坐标依次为1,2,3,…,n,n+1.过点P1,P2,P3,…,Pn,Pn+1分别作x轴、y轴的垂线段,构成如图所示的若干个矩形,将图中阴影部分的面积从左至右依次记为 ,
, ,
, ,…,
,…, ,则点P1的坐标为 ;
,则点P1的坐标为 ; = ;
= ; = .(用含n的代数式表示)
= .(用含n的代数式表示)

 的图象经过A(2,0)B(0,-6)两点.求这个二次函数的表达式.
的图象经过A(2,0)B(0,-6)两点.求这个二次函数的表达式. ”你认为正确吗?如果正确,说明理由;如果不正确,写出正确的解答过程.
”你认为正确吗?如果正确,说明理由;如果不正确,写出正确的解答过程.