题目内容
11.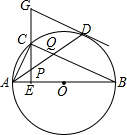 如图,在⊙O中.AB是直径,点D是⊙O上-点.点C是$\widehat{AD}$的中点,CE⊥AB于点E,在EC的延长线上有一点G,使GP=GD.连接AD,分别交CE、CB于点P、Q,连接AC,且AC=6,BC=8.
如图,在⊙O中.AB是直径,点D是⊙O上-点.点C是$\widehat{AD}$的中点,CE⊥AB于点E,在EC的延长线上有一点G,使GP=GD.连接AD,分别交CE、CB于点P、Q,连接AC,且AC=6,BC=8.(1)求证:GD是⊙O的切线;
(2)求线段AQ的长.
分析 (1)连接OD,利用等腰三角形的性质,可得出∠GPD=∠GDP,∠OAD=∠ODA,进一步证得∠APF+∠OAD=∠GDP+∠ODA=90°,即OD⊥GD,即可证得GD是⊙O的切线;
(2)证得△ACQ∽△BCA,根据相似三角形的性质即可求得.
解答 解:(1)连接OD,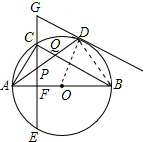
∵GP=GD,
∴∠GPD=∠GDP,
∴∠APF=∠GDP,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠APF+∠OAD=∠GDP+∠ODA,
∵CE⊥AB于点E,
∴∠APF+∠OAD=90°,
∴∠GDP+∠ODA=90°,
即∠ODG=90°,
∴OD⊥GD,
∴GD是⊙O的切线;
(2)∵C点C是$\widehat{AD}$的中点,
∴$\widehat{AC}$=$\widehat{CD}$,
∴∠ABC=∠DBC,
∵∠CAD=∠DBC,
∴∠CAD=∠ABC,
∵∠ACQ=∠BCA,
∴△ACQ∽△BCA,
∴$\frac{AQ}{AB}$=$\frac{AC}{BC}$,
∵AB为圆O的直径,
∴∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴$\frac{AQ}{10}$=$\frac{6}{8}$,
∴AQ=$\frac{15}{2}$.
点评 本题考查了切线的判定,圆周角定理,相似三角形的判定与性质,熟练掌握性质及定理是解决本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
1. 如图,正方形ABCD的对角线AC、BD相交于点O,OA=3,则此正方形的面积为( )
如图,正方形ABCD的对角线AC、BD相交于点O,OA=3,则此正方形的面积为( )
 如图,正方形ABCD的对角线AC、BD相交于点O,OA=3,则此正方形的面积为( )
如图,正方形ABCD的对角线AC、BD相交于点O,OA=3,则此正方形的面积为( )| A. | 3$\sqrt{2}$ | B. | 12 | C. | 18 | D. | 36 |
16.实验中学八年级(1)班50名学生参加期末考试,全班学生的数学成绩统计如表:
请根据表中提供的信息解答下列问题:
(1)该班学生这次考试数学成绩的众数是88分;
(2)该班学生这次考试数学成绩的中位数是86分;
(3)该班张华同学在这次考试中的数学成绩是83分,能不能说张华同学的数学成绩处于全班中游偏上水平?试说明理由.
| 成绩(分) | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 | 91 | 92 | 94 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 | 3 | 3 | 2 |
(1)该班学生这次考试数学成绩的众数是88分;
(2)该班学生这次考试数学成绩的中位数是86分;
(3)该班张华同学在这次考试中的数学成绩是83分,能不能说张华同学的数学成绩处于全班中游偏上水平?试说明理由.
3.近年来,某市水产养殖得到迅猛发展,水产养殖业已成为沿海某些城镇的支柱产业之一,某养殖场2014年养殖了20亩紫菜,平均每亩紫菜的常量为300kg,根据市场需要,2015年该养殖扩大养殖面积.并且全部养殖高产的新品种,已知紫菜养殖面积的增长率是平均每亩产量增长率的2倍,2015年紫菜的总产量为18000kg,设紫菜平均每亩产量的增长率为x.
(1)完成下表(用含x的代数式表示2015年的平均每亩产量和养殖面积):
(2)求紫菜平均每亩产量的增长率x.
(1)完成下表(用含x的代数式表示2015年的平均每亩产量和养殖面积):
| 年份 品种 | 2014年 | 2015年 |
| 平均每亩产量(kg) | 300 | 300(1+x) |
| 养殖面积(亩) | 20 | 20(1+2x) |
1.绝对值最小的有理数是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 不存在 |
 如图,A(-4,0),B(0,2),C(0,4).点D为x轴上一点,CD交直线AB于P,若△AOB≌△COD,求点P的坐标.
如图,A(-4,0),B(0,2),C(0,4).点D为x轴上一点,CD交直线AB于P,若△AOB≌△COD,求点P的坐标.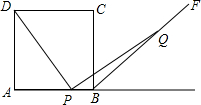 如图,正方形ABCD中,P为边AB上一动点,BF是∠ABC的外角平分线,Q是BF上一点,且PQ=DP,那么DP与PQ是否一定满足垂直关系?说明理由.
如图,正方形ABCD中,P为边AB上一动点,BF是∠ABC的外角平分线,Q是BF上一点,且PQ=DP,那么DP与PQ是否一定满足垂直关系?说明理由.