题目内容
 在一条笔直的道路上有相距9千米的A,B两地,甲以3km/h的速度从A地走向B地,出发0.5h后,乙从B地以4.5km/h的速度走向A地,甲、乙两人走到各自终点停止.设甲行走的时间为t(h).
在一条笔直的道路上有相距9千米的A,B两地,甲以3km/h的速度从A地走向B地,出发0.5h后,乙从B地以4.5km/h的速度走向A地,甲、乙两人走到各自终点停止.设甲行走的时间为t(h).(1)分别写出甲、乙两人与A地的距离s与时间t的函数表达式,并写出相应的t的取值范围;
(2)在同一直角坐标系中画出(1)中的两个函数的图象;
(3)当t为何值时,甲、乙两人相距不大于3.75km.
考点:一次函数的应用
专题:
分析:(1)由行程问题的数量关系路程=速度×时间就可以得出s与t的关系式;
(2)由列表法通过列表、描点及连线的过程就可以画出函数图象;
(3)由相遇问题的数量关系建立不等式组求出其解即可.
(2)由列表法通过列表、描点及连线的过程就可以画出函数图象;
(3)由相遇问题的数量关系建立不等式组求出其解即可.
解答:解:(1)由题意,得
s甲=3t(0≤t≤3),
s乙=9-4.5(t-0.5),
s乙=-4.5t+
(0≤t≤2.5).
(2)列表为:
描点并连线为:

(3)由题意,得
,
解得:1≤t≤2.
答:当1≤t≤2时甲、乙两人相距不大于3.75km.
s甲=3t(0≤t≤3),
s乙=9-4.5(t-0.5),
s乙=-4.5t+
| 45 |
| 4 |
(2)列表为:
| t | 0 | 2.5 | 3 | ||||
| s=3t | 0 | 9 | |||||
s=-4.5t+
|
| 0 |

(3)由题意,得
|
解得:1≤t≤2.
答:当1≤t≤2时甲、乙两人相距不大于3.75km.
点评:本题考查了行程问题的数量关系的运用,一次函数的解析式的运用,列表法画函数图象的运用,一元一次不等式组的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
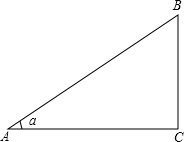 如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )
如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )| A、10tana(米) | ||||||
B、
| ||||||
| C、10sina(米) | ||||||
D、
|
如果4x=5y(y≠0),那么下列比例式成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
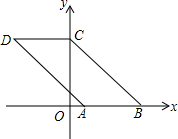 如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( ) 如图,A,B,C,D是⊙O上不同四点,OA⊥BC,∠AOB=60°,则∠ADC=
如图,A,B,C,D是⊙O上不同四点,OA⊥BC,∠AOB=60°,则∠ADC=