题目内容
如图所示，直线l1∥l2，∠1=40°，则∠2为
- A.140°
- B.30°
- C.40°
- D.60°
C
分析：根据平行线的性质：两直线平行，同位角相等，可求得∠1的同位角∠3为40°，又因为∠2与∠3是对顶角，所以∠2=40°．
解答：
解：∵l1∥l2，
∴∠3=∠1=40°，
∴∠2=∠3=40°．
故选C．
点评：本题考查的是平行线的性质以及对顶角的性质，解题的关键是找出∠1的同位角．
分析：根据平行线的性质：两直线平行，同位角相等，可求得∠1的同位角∠3为40°，又因为∠2与∠3是对顶角，所以∠2=40°．
解答：
解：∵l1∥l2，∴∠3=∠1=40°，
∴∠2=∠3=40°．
故选C．
点评：本题考查的是平行线的性质以及对顶角的性质，解题的关键是找出∠1的同位角．
练习册系列答案
轻松暑假总复习系列答案
相关题目
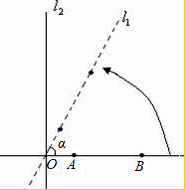如图所示，直线L1⊥L2，垂足为点O，A，B是直线L1上的两点，且OB=2，AB=
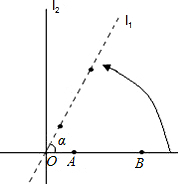角形，请用不等式表示α的取值范围：
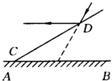44、如图所示，直线L1∥L2，C1，C2，C3是L1上的三点，连接C1A，C1B，C2A，C2B，C3A，C3B，得△C1AB，△C2AB，△C3AB，试说明△C1AB，△C2AB，△C3AB的面积相等．
2、如图所示，直线l1∥l2，∠1=40°，则∠2为（ ）