题目内容
【题目】某公司生产某环保产品的成本为每件40元,经过市场调研发现:这件产品在未来两个月![]() 天
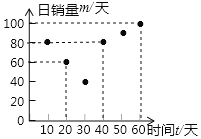
天![]() 的日销量
的日销量![]() 件
件![]() 与时间
与时间![]() 天
天![]() 的关系如图所示
的关系如图所示![]() 未来两个月
未来两个月![]() 天
天![]() 该商品每天的价格
该商品每天的价格![]() 元
元![]() 件
件![]() 与时间
与时间![]() 天
天![]() 的函数关系式为:
的函数关系式为: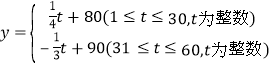
根据以上信息,解决以下问题:
![]() 请分别确定
请分别确定![]() 和
和![]() 时该产品的日销量
时该产品的日销量![]() 件
件![]() 与时间
与时间![]() 天
天![]() 之间的函数关系式;
之间的函数关系式;
![]() 请预测未来第一月日销量利润
请预测未来第一月日销量利润![]() 元
元![]() 的最小值是多少?第二个月日销量利润
的最小值是多少?第二个月日销量利润![]() 元
元![]() 的最大值是多少?
的最大值是多少?
![]() 为创建“两型社会”,政府决定大力扶持该环保产品的生产和销售,从第二个月开始每销售一件该产品就补贴a元
为创建“两型社会”,政府决定大力扶持该环保产品的生产和销售,从第二个月开始每销售一件该产品就补贴a元![]() 有了政府补贴以后,第二个月内该产品日销售利润
有了政府补贴以后,第二个月内该产品日销售利润![]() 元
元![]() 随时间
随时间![]() 天
天![]() 的增大而增大,求a的取值范围.
的增大而增大,求a的取值范围.
【答案】![]() ;
;![]() 时,
时,![]() 的最大值为
的最大值为![]() 元;(3)
元;(3)![]() 时,W随t的增大而增大.
时,W随t的增大而增大.
【解析】
![]() 利用待定系数法即可解决问题;
利用待定系数法即可解决问题;
![]() 分别构建二次函数,利用二次函数的性质即可解决问题;
分别构建二次函数,利用二次函数的性质即可解决问题;
![]() 构建二次函数,利用二次函数的性质即可解决问题;
构建二次函数,利用二次函数的性质即可解决问题;
解:![]() 当
当![]() 时,设
时,设![]() ,则有
,则有![]() ,
,
解得![]() ,
,
![]() ,
,
当![]() 时,设
时,设![]() ,则有
,则有![]() ,
,
解得![]() ,
,
![]() .
.
![]() 由题意
由题意![]() ,
,
当![]() 时,
时,![]() 有最小值
有最小值![]() 元
元![]() ,
,
![]() ,
,
![]() 时,
时,![]() 的最大值为
的最大值为![]() 元
元![]()
![]() 由题意
由题意![]() ,
,
对称轴![]() ,
,
![]() ,
,
![]() 的取值范围在对称轴的左侧时W随t的增大而增大,
的取值范围在对称轴的左侧时W随t的增大而增大,
![]() 当
当![]() ,
,
![]() ,
,
即![]() 时,W随t的增大而增大.
时,W随t的增大而增大.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.