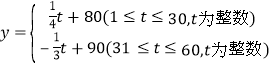Question

【题目】已知二次函数与一次函数，令.

（1）若的函数图象相交于轴上的同一点．

①求的值；

②当为何值时，的值最小，试求出该最小值．

（2）当时，随的增大而减小，请写出的大小关系并给予证明．

Answer 1

【答案】（1）①②（2）

【解析】分析：（1）①直接得出一次函数y2=x+1过（-1，0），进而代入二次函数解析式得出答案；

②直接利用m的值得出M与x的函数关系式，进而得出最值；

（2）①首先表示出二次函数的对称轴，进而二次函数增减性得出m的取值范围；

②首先得出当x=-2时，M的值，进而得出M＜M0≤0，即y1-y2＜0，即可得出答案．

详解：（1）① 、的函数图象交于x轴上的同一点,

一次函数过点

二次函数为常数且也过点

解得: ;

②

,

当时，的值最小，最小值为

（2）

证明：

对称轴为

且随的增大而减小，

当时，

又且随的增大而减小，