题目内容
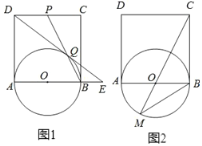
【题目】已知正方形ABCD的对角线AC与BD交于点O，点E、F分别是线段OB、OC上的动点
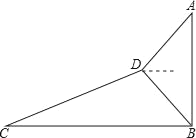
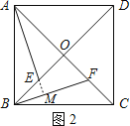
（1）如果动点E、F满足BE＝OF（如图），且AE⊥BF时，问点E在什么位置？并证明你的结论；
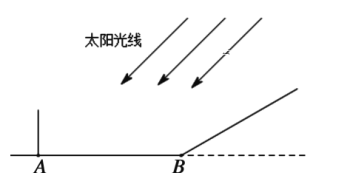
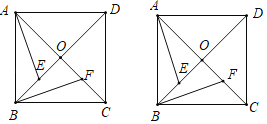
（2）如果动点E、F满足BE＝CF（如图），写出所有以点E或F为顶点的全等三角形（不得添加辅助线）．
【答案】（1）当AE⊥BF时，点E在BO中点，见解析；（2）以点E或F为顶点的全等三角形有△ABE≌△BCF，△AOE≌△BOF，△ADE≌△BAF.
【解析】
（1）根据正方形性质及已知条件得出△BEM∽△AEO，△BEM∽△BOF，再根据三角形相似的性质即可得出答案；
（2）根据正方形性质及BE＝CF即可得出全等的三角形．
解：（1）当
时，点
在
中点．证明如下：
延长
交
于点
，如图所示：
，
，
，
，
，
，
，
，
，
，
，
，
故当时，点在中点；
（2）
四边形
是正方形，
，
，
，
，
，
，
，
，
，
，
在△ABE和△BCF中，
，
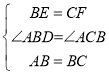同理可得
，
；
以点或
为顶点的全等三角形有
，，；
练习册系列答案
阅读快车系列答案
相关题目
