题目内容
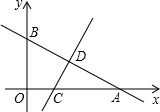 如图,一次函数y=-
如图,一次函数y=-
| ||
| 3 |
| 3 |
(1)求点C的坐标;
(2)在射线DC上求一点P,使得PC=AC,求出点P的坐标;
(3)在坐标平面内,是否存在点Q(除点C外),使得以A、D、Q为顶点的三角形与△ACD全等?若存在,请求出所有符合条件的点Q的坐标;若不存在,请说明理.
分析:(1)首先求出图象与坐标轴交点坐标,进而借助勾股定理得出OC的长,即可得出C点坐标;
(2)当PC=AC=4,借助勾股定理得出OP的长即可得出答案;
(3)首先得出Q点坐标,进而利用当△ACD≌△DQ′A时,当△ACD≌△DQ″A时,当△ACD≌△AQD时,分别得出符合条件的点的坐标即可.
(2)当PC=AC=4,借助勾股定理得出OP的长即可得出答案;
(3)首先得出Q点坐标,进而利用当△ACD≌△DQ′A时,当△ACD≌△DQ″A时,当△ACD≌△AQD时,分别得出符合条件的点的坐标即可.
解答: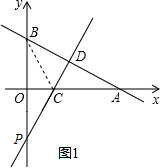 解:(1)如图1,连接BC.
解:(1)如图1,连接BC.
∵一次函数y=-
x+2
的图象与坐标轴分别交于点 A和B两点,
当y=0,则x=6,当x=0,则y=2
,
∴A(6,0),B(0,2
).
设OC=x,则AC=CB=6-x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
(2
)2+x2=(6-x)2,
解得x=2,
∴C点坐标为:(2,0);
(2)如图1,∵AC=OA-OC=6-2=4,CO=2,
∴当PC=AC=4,
∴OP=
=2
,
∴P点坐标为:(0,-2
);
(3)如图2,
∵△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D,
∴D点坐标为AB中点,∠CDA=90°,
∵A(6,0),B(0,2
),
∴D点坐标为:(3,
),
∴EC=3-2=1,DE=
,CD=2,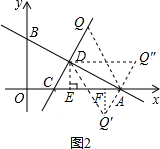
∴tan∠DCE=
,
∴∠DCE=60°,
∴∠DAC=30°,
当△ACD≌△DQ′A时,
∴∠Q′=∠Q′AO=60°,
∴AQ′=2,
∴AF=1,FQ′=
,
可得Q′横坐标为:5,纵坐标为:-
,
∴Q′点坐标为;(5,-
);
当△ACD≌△AQD时,
则D为QC中点,
∵D点坐标为(3,
),CE=1,
∴Q点横坐标为:2+1+1=4,
∴Q点坐标为:(4,2
),
当△ACD≌△DQ″A时,
∵∠CAD=∠ADQ″,
∴AC
DQ″,
∵AC=4,D点坐标为(3,
),
∴Q″点横坐标为:3+4=7,
∴Q″点坐标为:(7,
),
综上所述:所有符合条件的点Q的坐标为:(4,2
) (7,
) (5,-
).
 解:(1)如图1,连接BC.
解:(1)如图1,连接BC.∵一次函数y=-
| ||
| 3 |
| 3 |
当y=0,则x=6,当x=0,则y=2
| 3 |
∴A(6,0),B(0,2
| 3 |
设OC=x,则AC=CB=6-x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
(2
| 3 |
解得x=2,
∴C点坐标为:(2,0);
(2)如图1,∵AC=OA-OC=6-2=4,CO=2,
∴当PC=AC=4,
∴OP=
| 42-22 |
| 3 |
∴P点坐标为:(0,-2
| 3 |
(3)如图2,
∵△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D,
∴D点坐标为AB中点,∠CDA=90°,
∵A(6,0),B(0,2
| 3 |
∴D点坐标为:(3,
| 3 |
∴EC=3-2=1,DE=
| 3 |

∴tan∠DCE=
| 3 |
∴∠DCE=60°,
∴∠DAC=30°,
当△ACD≌△DQ′A时,
∴∠Q′=∠Q′AO=60°,
∴AQ′=2,
∴AF=1,FQ′=
| 3 |
可得Q′横坐标为:5,纵坐标为:-
| 3 |
∴Q′点坐标为;(5,-
| 3 |
当△ACD≌△AQD时,
则D为QC中点,
∵D点坐标为(3,
| 3 |
∴Q点横坐标为:2+1+1=4,
∴Q点坐标为:(4,2
| 3 |
当△ACD≌△DQ″A时,
∵∠CAD=∠ADQ″,
∴AC
| ∥ |
. |
∵AC=4,D点坐标为(3,
| 3 |
∴Q″点横坐标为:3+4=7,
∴Q″点坐标为:(7,
| 3 |
综上所述:所有符合条件的点Q的坐标为:(4,2
| 3 |
| 3 |
| 3 |
点评:此题主要考查了一次函数综合以及勾股定理的应用和全等三角形的性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数