Question

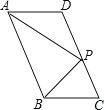
【题目】如图，在平行四边形ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的面积是_______．

Answer 1

【答案】24

【解析】

根据平行四边形性质得出AD∥CB，AB∥CD，推出∠DAB＋∠CBA＝180°，求出∠PAB＋∠PBA＝90°，在△APB中求出∠APB＝90°，由勾股定理求出BP，证出AD＝DP＝5，BC＝PC＝5，得出DC＝10＝AB，即可求出答案．

∵四边形ABCD是平行四边形，

∴AD∥CB，AB∥CD，

∴∠DAB＋∠CBA＝180°，

又∵AP和BP分别平分∠DAB和∠CBA，

∴∠PAB＋∠PBA＝（∠DAB＋∠CBA）＝90°，

在△APB中，∠APB＝180°（∠PAB＋∠PBA）＝90°；

∵AP平分∠DAB，

∴∠DAP＝∠PAB，

∵AB∥CD，

∴∠PAB＝∠DPA

∴∠DAP＝∠DPA

∴△ADP是等腰三角形，

∴AD＝DP＝5，

同理：PC＝CB＝5，

即AB＝DC＝DP＋PC＝10，

在Rt△APB中，AB＝10，AP＝8，

∴BP＝＝6，

∴△APB的面积＝6×8÷2＝24；

故答案为：24．