题目内容
17. 如图,将圆沿AB折叠后,圆弧恰好经过圆心,则∠AOB等于( )
如图,将圆沿AB折叠后,圆弧恰好经过圆心,则∠AOB等于( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
分析 过O点作OC⊥AB,垂足为D,交⊙O于点C,由折叠的性质可知OD为半径的一半,而OA为半径,可求∠A=30°,同理可得∠B=30°,在△AOB中,由内角和定理求∠AOB.
解答 解:过O点作OC⊥AB,垂足为D,交⊙O于点C.
由折叠的性质可知,OD=$\frac{1}{2}$OC=$\frac{1}{2}$OA,
由此可得,在Rt△AOD中,∠A=30°,
同理可得∠B=30°,
在△AOB中,由内角和定理,
得∠AOB=180°-∠A-∠B=120°,
故选:C.
点评 本题考查三角形的内角和,圆的有关知识的应用,求得∠OAB=∠OBA=30°是解题的关键.

练习册系列答案
相关题目
5.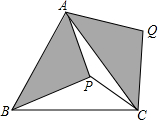 如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )
如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )
 如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )
如图,P是等边△ABC内部一点,把△ABP绕点A逆时针旋转,使点B与点C重合,得到△ACQ,则旋转角的度数是( )| A. | 70° | B. | 80° | C. | 60° | D. | 50° |
2. 实数a,b,c在数轴上的位置如图所示,下列各式错误的是( )
实数a,b,c在数轴上的位置如图所示,下列各式错误的是( )
 实数a,b,c在数轴上的位置如图所示,下列各式错误的是( )
实数a,b,c在数轴上的位置如图所示,下列各式错误的是( )| A. | a+b<0 | B. | a-b<0 | C. | a+c<0 | D. | b+c<0 |
 如图,O,B,C三点均在二次函数y=$\sqrt{3}{x}^{2}$的图象上,点O为坐标原点,四边形OBAC为菱形,且∠OBA=120°,试求菱形OBAC的面积.
如图,O,B,C三点均在二次函数y=$\sqrt{3}{x}^{2}$的图象上,点O为坐标原点,四边形OBAC为菱形,且∠OBA=120°,试求菱形OBAC的面积.