题目内容
13.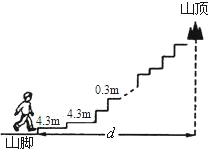 公园里有一座小山供游人健身锻炼,上山台阶的截面如图所示,从山脚至山顶的台阶高度起起伏伏,而宽度除前两个台阶为4.3m外,其余每个台阶宽都为0.3米.
公园里有一座小山供游人健身锻炼,上山台阶的截面如图所示,从山脚至山顶的台阶高度起起伏伏,而宽度除前两个台阶为4.3m外,其余每个台阶宽都为0.3米.(1)求山脚至山顶的水平距离d(米)与台阶个数n(n≥2)之间的函数关系式(不要求写自变量取值范围);
(2)若从山脚到山顶的台阶总数为1200个,求山脚到山顶的水平距离d.
分析 (1)根据山脚至山顶的水平距离d等于n级台阶的宽度之和,列式可得:d=4.3×2+0.3×(n-2);
(2)将n=1200代入(1)中所求的式子,即可求出d的值
解答 解:(1)依题意得
d=4.3×2+0.3×(n-2),
即d=0.3n+8;
(2)当n=1200时,d=0.3×1200+8=368(米),
故山脚到山顶的水平距离是368米.
点评 此题考查实际问题中函数关系的求法.主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解.

练习册系列答案
相关题目
18.在三边分别为下列长度的三角形中,不是直角三角形的为( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 2,3,$\sqrt{5}$ | C. | 5,13,12 | D. | 4,7,5 |
2.下列句子,不是命题的是( )
| A. | 两条直线平行,同位角相等 | B. | 直线AB垂直于CD吗? | ||
| C. | 若|a|=|b|,那么a2=b2 | D. | 对顶角相等 |
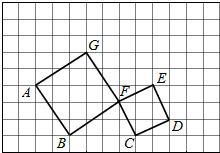 如图,建立平面直角坐标系,正方形ABFG和正方形CDEF中,使点B、C的坐标分别为(-4,0)和(0,0)
如图,建立平面直角坐标系,正方形ABFG和正方形CDEF中,使点B、C的坐标分别为(-4,0)和(0,0)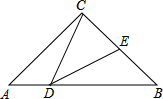 如图,在△ABC中,已知AB=8,AC=BC=5,点D是边AB上的一个动点,连结CD,作∠CDE=∠A,边DE与BC交于点E.
如图,在△ABC中,已知AB=8,AC=BC=5,点D是边AB上的一个动点,连结CD,作∠CDE=∠A,边DE与BC交于点E.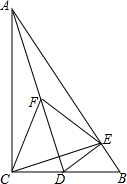 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.