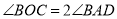题目内容
请你画出一个以BC为底边的等腰ΔABC,使底边上的高AD=BC.
(1)求tanB和 sinB的值;
(2)在你所画的等腰ΔABC中设底边BC=5米,求腰上的高BE.
如图,正确画出图形, (1)∵AB=AC,AD⊥BC,AD=BC, ∴BD=BC=AD.即AD=2BD. ∴AB=BD. ∴tanB=, sinB=. (2)在Rt△BEC中,sinC=sin∠ABC=, 又∵sinC=, ∴. 故(米). 【解析】(1)本题可根据三角形的特殊性(等腰三角形)和AD=BC,先求出AD和BD,CD的关系,进...
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
探究函数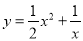 的图象与性质,下面是探究过程,请补充完整:
的图象与性质,下面是探究过程,请补充完整:
( )下表是
)下表是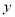 与
与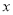 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
函数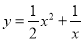 的自变量
的自变量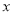 的取值范围是__________,
的取值范围是__________, 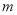 的值为__________.
的值为__________.
(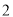 )描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
)描出以上表中各对对应值为坐标的点,并画出该函数的大致图象.
(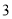 )进一步探究函数图象发现:
)进一步探究函数图象发现:
①函数图象与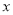 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程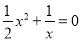 有__________个实数根.
有__________个实数根.
②方程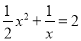 有__________个实数根.
有__________个实数根.
③结合函数的图象,写出该函数的一条性质__________.

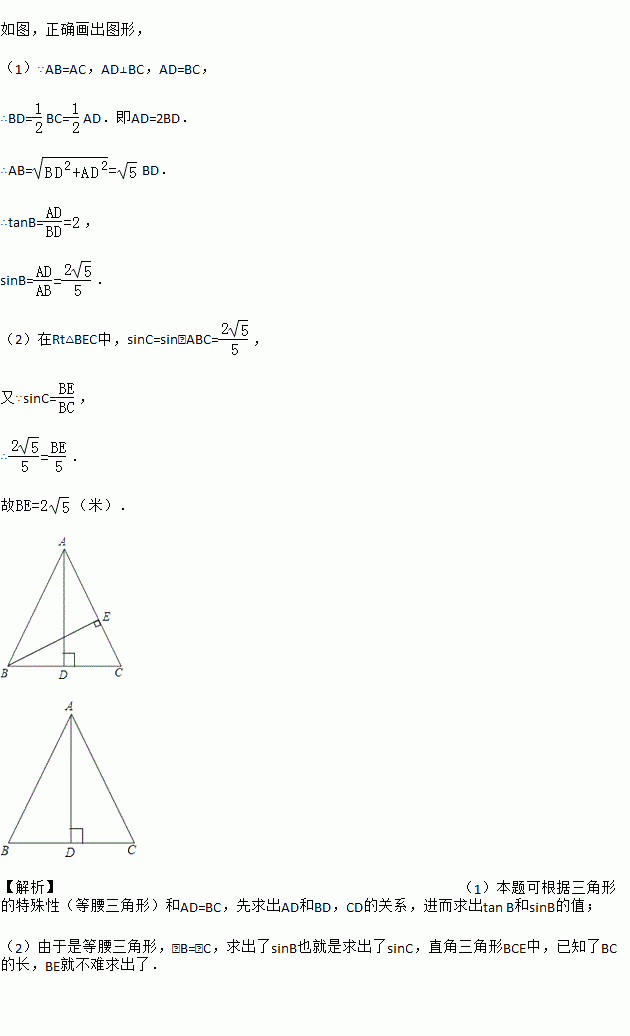

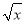 ,|x﹣2|}.若动直线y=m与函数y=f(x)的图象有三个交点,它们的横坐标分别为x1、x2、x3 , 则x1x2x3的最大值为________.
,|x﹣2|}.若动直线y=m与函数y=f(x)的图象有三个交点,它们的横坐标分别为x1、x2、x3 , 则x1x2x3的最大值为________. 的值可能是( )
的值可能是( )
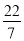 ,﹣22
,﹣22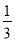 ,﹣2.55555…,3.01,+9,﹣2π.+10%,4.020020002…(每两个2之间依次增加1个0),
,﹣2.55555…,3.01,+9,﹣2π.+10%,4.020020002…(每两个2之间依次增加1个0),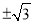
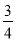 ,则梯子AB的长度为______米.
,则梯子AB的长度为______米.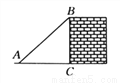
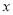

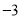
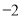
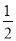
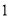
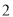
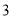


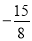
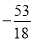
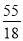
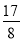
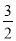
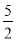
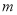

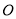 中,
中, 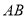 是直径,
是直径, 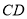 是弦,
是弦, 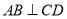 ,垂足为
,垂足为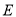 ,连接
,连接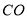 ,
, 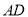 ,
, 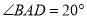 ,则下列说法中正确的是( ).
,则下列说法中正确的是( ).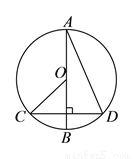
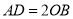 B.
B. 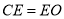 C.
C. 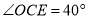 D.
D.