题目内容
9.双曲线y=$\frac{k}{x}$(k≠0)经过点(a,b),则它不经过的点是( )| A. | (b,a) | B. | (-a,-b) | C. | (2a,$\frac{b}{2}$) | D. | (-b,a) |
分析 双曲线y=$\frac{k}{x}$(k≠0)经过点(a,b),得k=ab,把各点的坐标相乘,如果为k,则这点在双曲线上,否则,不在双曲线上.
解答 解:∵双曲线y=$\frac{k}{x}$(k≠0)经过点(a,b),
∴k=ab,
A.ba=k,(b,a)在双曲线上,
B.(-a)•(-b)=k,(-a,-b)在双曲线上,
C.2a•$\frac{b}{2}$=k,(2a,$\frac{b}{2}$在双曲线上,
D.(-b)•a=-ab=-k,(-b,a)不在双曲线上,
故选D.
点评 本题主要考查了反比例函数的意义,熟练把握反比例函数的意义是解题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
17.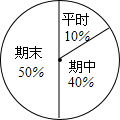 小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.
小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.
如果学期总评成绩按扇形图所示的权重计算,小军上学期的总评成绩是109.7分.
 小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.
小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.| 测验类别 | 平时 | 期中考试 | 期末考试 | |||
| 测验1 | 测验2 | 测验3 | 测验4 | |||
| 成绩 | 110 | 105 | 95 | 110 | 108 | 112 |
1.已知一次函数y=(1-2k)x+k的图象经过第一、二、三象限,则k的取值范围是( )
| A. | k>0 | B. | k<0 | C. | 0<k<$\frac{1}{2}$ | D. | k<$\frac{1}{2}$ |
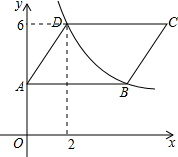 如图,平行四边形ABCD的顶点B,D都在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( )
如图,平行四边形ABCD的顶点B,D都在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(2,6),AB平行于x轴,点A的坐标为(0,3),将这个平行四边形像左平移2个单位,再向下平移3个单位后,点C的坐标为( )