题目内容
15．如果两个相似三角形的面积的比是9：4，其中较小的三角形的周长为8，那么较大的三角形的周长的是12．分析 先求出相似三角形的相似比，再求出两三角形的周长比，代入求出即可．
解答 解：设较大的三角形的周长为x，
∵两个相似三角形的面积的比是9：4，
∴这两个相似三角形的相似比为3：2，
∴这两个三角形的周长比为3：2，
∵较小的三角形的周长为8，
∴$\frac{3}{2}$=$\frac{x}{8}$，
∴x=12，
故答案为：12．
点评 本题考查了相似三角形的性质的应用，能熟记相似三角形的性质是解此题的关键，注意：相似三角形的面积比等于相似比的平方，周长比等于相似比．
练习册系列答案
相关题目
18．
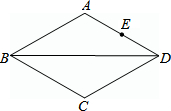如图，在菱形ABCD中，AB=4，∠ABC=60°，E为AD中点，P为对角线BD上一动点，连结PA和PE，则PA+PE的值最小是（ ）
如图，在菱形ABCD中，AB=4，∠ABC=60°，E为AD中点，P为对角线BD上一动点，连结PA和PE，则PA+PE的值最小是（ ）| A． | 2 | B． | 4 | C． | $\sqrt{3}$ | D． | $2\sqrt{3}$ |
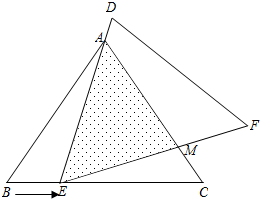如图，在△ABC中，己知AB=AC=5，BC=6，且将△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．
3．下列各式的约分，正确的是（ ）
| A． | $\frac{-a-b}{a-b}$=1 | B． | $\frac{-a-b}{a-b}$=-1 | C． | $\frac{{a}^{2}-{b}^{2}}{a+b}$=a-b | D． | $\frac{{a}^{2}-{b}^{2}}{a+b}$=a+b |