题目内容
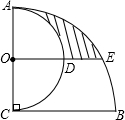
如图，AB是⊙O的直径，BC是⊙O的弦，半径OD⊥BC，垂足为E，若BC=6
，DE=3．
求：（1）⊙O的半径；（2）弦AC的长；（3）阴影部分的面积．
| 3 |
求：（1）⊙O的半径；（2）弦AC的长；（3）阴影部分的面积．
（1）∵半径OD⊥BC，
∴CE=BE，
∵BC=6
，
∴CE=3
，
设OC=x，在直角三角形OCE中，OC2=CE2+OE2，
∴x2=（3
）2+（x-3）2，
∴x=6
即半径OC=6；（4分）
（2）∵AB为直径，
∴∠ACB=90°，AB=12，
又∵BC=6
，
∴AC2=AB2-BC2=36，
∴AC=6；（7分）
（3）∵OA=OC=AC=6，
∴∠AOC=60°，
∴S阴=S扇-S△OAC=
-
×6×6×
=6π-9
．（10分）
∴CE=BE，
∵BC=6
| 3 |
∴CE=3
| 3 |
设OC=x，在直角三角形OCE中，OC2=CE2+OE2，
∴x2=（3
| 3 |
∴x=6
即半径OC=6；（4分）
（2）∵AB为直径，
∴∠ACB=90°，AB=12，
又∵BC=6
| 3 |
∴AC2=AB2-BC2=36，
∴AC=6；（7分）
（3）∵OA=OC=AC=6，
∴∠AOC=60°，
∴S阴=S扇-S△OAC=
| 60×π×62 |
| 360 |
| 1 |
| 2 |
| ||
| 2 |
=6π-9
| 3 |
练习册系列答案
相关题目
