题目内容
一次函数y=kx+b,则k、b的值为( )

|
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
考点:
一次函数图象与系数的关系.
分析:
根据图象在坐标平面内的位置关系确定k,b的取值范围,从而求解.
解答:
解:∵一次函数y=kx+b的图象经过第二、四象限,
∴k<0时,
又∵直线与y轴正半轴相交,
∴b>0.
故k<0,b>0.
故选C.
点评:
本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.
k>0时,直线必经过一、三象限;
k<0时,直线必经过二、四象限;
b>0时,直线与y轴正半轴相交;
b=0时,直线过原点;
b<0时,直线与y轴负半轴相交.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
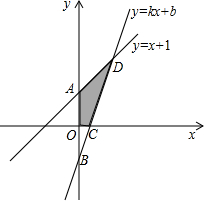 x轴以及y=x+1的图象分别交于点C、D.
x轴以及y=x+1的图象分别交于点C、D.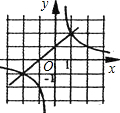 一次函数y=kx+b与反比例函数y=
一次函数y=kx+b与反比例函数y= (2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,
(2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,