��Ŀ����
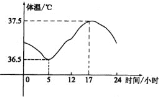
����Ŀ����ͼ��ʾ����ֱ֪��![]() ��
��![]() �ཻ��
�ཻ��![]() ��
��![]() ������
������![]() ��
��![]() λ����ʼ���Ƶ�
λ����ʼ���Ƶ�![]() ��ʱ����ת���ձ�
��ʱ����ת���ձ�![]() ��ʼ��
��ʼ��![]() �γɵĽǶ�Ϊ
�γɵĽǶ�Ϊ![]() .
.
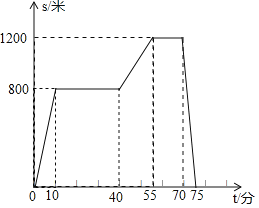
����1����![]() ��ʱ����ת
��ʱ����ת![]() ֹͣ����
ֹͣ����
��1��![]() __________________ʱ��
__________________ʱ��![]() ƽ��
ƽ��![]() ��
��
��2��![]() __________________ʱ��
__________________ʱ��![]() ��
��
��3��![]() __________________ʱ��
__________________ʱ��![]() ��
��
����2����![]() ��ʱ����ת���ٶ�Ϊÿ��
��ʱ����ת���ٶ�Ϊÿ��![]() ����
����![]() ������ת��ͬʱ��ֱ��
������ת��ͬʱ��ֱ��![]() Ҳ��ͼ��λ�ÿ�ʼ�Ƶ�
Ҳ��ͼ��λ�ÿ�ʼ�Ƶ�![]() ��ʱ��������ת����ת�ٶ�Ϊÿ��
��ʱ��������ת����ת�ٶ�Ϊÿ��![]() ����
����![]() �����תһ��ʱ��
�����תһ��ʱ��![]() Ҳͬʱֹͣ��ת.����תʱ��Ϊ
Ҳͬʱֹͣ��ת.����תʱ��Ϊ![]() ��
��![]() ����.
����.
��1����תʱ��![]() Ϊ����ʱ������
Ϊ����ʱ������![]() ��
��![]() �غ�.��д��������.
�غ�.��д��������.
��2���۲���תȫ���̣��ж���תʱ��![]() Ϊ����ʱ������
Ϊ����ʱ������![]() ƽ��
ƽ��![]() .��ֱ��д��
.��ֱ��д��![]() ��ֵ.��ע��
��ֵ.��ע��![]() ָ����
ָ����![]() ��С��
��С��![]() �Ľǣ�
�Ľǣ�
���𰸡�����1����1��![]() ��2��
��2��![]() 150������3��
150������3��![]() =40����120��������2����1��t=20�룻��2��t=
=40����120��������2����1��t=20�룻��2��t=![]() ��.
��.
��������
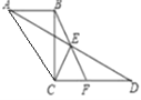
����1����1������![]() �ͽ�ƽ���߶��弴�ɽ��
�ͽ�ƽ���߶��弴�ɽ��
(2)�ɴ�ֱ����֪����POC=90�㣬��Ϊ![]() ���ɵ�
���ɵ�![]() =��POC+
=��POC+![]() .
.
��3��![]() =40���90�㡣Ӧ������������ۣ�
=40���90�㡣Ӧ������������ۣ�
�ڵ�����OP�ڡ�BOC�ڲ�ʱ������![]() ���ɽ��
���ɽ��
����2����1���������г������е������⣬������![]() ��
��![]() �غ�ʱ����AOC=��AOP
�غ�ʱ����AOC=��AOP
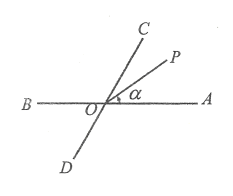
�⣺����1����1����Ϊ![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ��AOP=
��AOP=![]()
![]() =30�㣻
=30�㣻
��2��![]() 150��ʱ��
150��ʱ��![]() .
.
��Ϊ![]() ��OA��ʼ����ʱ����ת
��OA��ʼ����ʱ����ת![]() ֹͣ��������
ֹͣ��������![]() ������Ϊ
������Ϊ![]() ������
������![]() ��AOP=90��+60��=150��.
��AOP=90��+60��=150��.
��3��![]() =40���120�㡣�ٵ�����OP�ڡ�AOC�ڲ�ʱ����Ϊ
=40���120�㡣�ٵ�����OP�ڡ�AOC�ڲ�ʱ����Ϊ![]() ��
��![]() �����ԣ�
�����ԣ�![]() ��APO=
��APO=![]()
![]() =40�㣻
=40�㣻
�ڵ�����OP�ڡ�BOC�ڲ�ʱ����ͼ����Ϊ![]() ��
��![]() ������
������![]() ��APO=2
��APO=2 ![]() =120�㣻
=120�㣻

����2����1������תt��ʱ����AOP=8t����AOC=60��+5t����Ϊ����![]() ��
��![]() �غϣ����ԡ�AOP=��AOC����8t=60��+5t�����t=20����t=20��ʱ������
�غϣ����ԡ�AOP=��AOC����8t=60��+5t�����t=20����t=20��ʱ������![]() ��
��![]() �غ�.
�غ�.
��2��t��ʱ����AOC=60��+5t����AOP=8t��������![]() ƽ��
ƽ��![]() ʱ����AOP=
ʱ����AOP=![]()
![]() ����8t=
����8t=![]() ��60��+5t������ã�t=
��60��+5t������ã�t=![]() �����Ե�t=
�����Ե�t=![]() ��ʱ������
��ʱ������![]() ƽ��
ƽ��![]() .
.

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�