题目内容
【题目】(1)如图①,正方形![]() 的两边分别在正方形
的两边分别在正方形![]() 的边
的边![]() 和
和![]() 上,连接
上,连接![]() .填空:线段
.填空:线段![]() 与
与![]() 的数量关系为________;直线
的数量关系为________;直线![]() 与
与![]() 所夹锐角的大小为________.
所夹锐角的大小为________.



(2)如图②,将正方形![]() 绕点
绕点![]() 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
(3)把图②中的正方形都换成菱形,且![]() ,如图③,直接写出
,如图③,直接写出![]() ______.
______.
【答案】(1)①![]() ,②45°;(2)仍然成立,见解析;(3)
,②45°;(2)仍然成立,见解析;(3)![]()
【解析】
(1)根据正方形的性质即可得出答案;
(2)过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,并延长交
,并延长交![]() 、
、![]() 交于点
交于点![]() ,证明
,证明![]() ,接着证明四边形
,接着证明四边形![]() 是平行四边形,即可得出答案;
是平行四边形,即可得出答案;
(3)过![]() 作∠GDH=120°,且
作∠GDH=120°,且![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() ,接着证明四边形
,接着证明四边形![]() 是平行四边形,再过点D作DM⊥GH于点M,证出GM=
是平行四边形,再过点D作DM⊥GH于点M,证出GM=![]() GH=
GH=![]() CF,DM=
CF,DM=![]() DG,再利用勾股定理计算即可得出答案.
DG,再利用勾股定理计算即可得出答案.
解:(1)①线段![]() 与
与![]() 的数量关系为
的数量关系为![]() ;
;
②直线![]() 与
与![]() 所夹锐角的度数为45°.
所夹锐角的度数为45°.
连接AF,根据正方形的性质可得A、F、C三点共线,∠CAD=45°
∵AF=![]() AG,AC=
AG,AC=![]() AD
AD
∴CF=AC-AF=![]() (AD-AG)=
(AD-AG)=![]() DG
DG
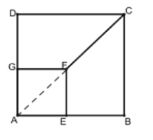
(2)仍然成立,证明如下:
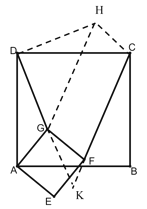
过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,并延长交
,并延长交![]() 、
、![]() 交于点
交于点![]()
∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,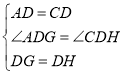
∴![]() ,
,
∴![]() ,
,![]()
∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]() ,∴
,∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,
![]() ,
,
∴![]()
∴![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]()
在![]() 中,
中,![]()
∴![]() ,
,
即![]() ,
,
∵![]()
∴![]() ,即直线
,即直线![]() 与
与![]() 所夹锐角的度数为45°;
所夹锐角的度数为45°;
(3)过![]() 作∠GDH=120°,且
作∠GDH=120°,且![]() ,连接
,连接![]() ,
,![]()
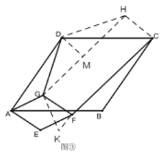
∵四边形![]() 是菱形 ,
是菱形 ,![]()
∴![]() ,∠ADC=120°
,∠ADC=120°
∵∠GDH=120°
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,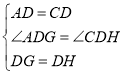
∴![]() ,
,
∴![]() ,
,![]()
∵四边形![]() 是菱形
是菱形
∴![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,
![]() ,
,
∴![]()
∴![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]()
过点D作DM⊥GH于点M
∴GM=![]() GH=
GH=![]() CF,DM=
CF,DM=![]() DG
DG
在Rt△DGM中,![]()
∴GM=![]() DG,
DG,
∴DG:CF=![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 饮料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?