Question

【题目】已知是直角三角形，，，直线经过点，分别过点、向直线作垂线，垂足分别为、.

（1）如图1，当点，位于直线的同侧时，证明：.

（2）如图2，若点，在直线的异侧，其它条件不变，是否依然成立？请说明理由.

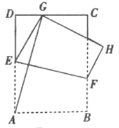
（3）图形变式：如图3，锐角中，，直线经过点，点，分别在直线上，点，位于的同一侧，如果，请找到图中的全等三角形，并直接写出线段，，的数量关系.

Answer 1

【答案】（1）详见解析；（2）详见解析；（3），.

【解析】

（1）易证∠ABD=∠CAE，由AAS即可得出△ABD≌△CAE；
（2）易证∠ABD=∠CAE，由AAS即可得出△ABD≌△CAE；
（3）由∠CEA=∠ADB=∠BAC，根据三角形内角和定理和平角的定义可得∠ECA+∠EAC=∠EAC+∠DAB，得出∠DAB=∠ECA，由AAS即可证得△ABD≌△CAE，得出AD=EC，DB=AE，则ED=EC+DB．

解：（1）在中，，

∵，∴，∴.

又∵，，

∴.

（2）在中，，

∵，∴，∴，

∵，，

∴.

（3），.

理由如下：
∵∠CEA=∠ADB=∠BAC，
∴∠ECA+∠EAC=∠EAC+∠DAB，
∴∠DAB=∠ECA，
在△ABD和△CAE中，

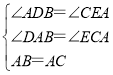
∴△ABD≌△CAE（AAS），
∴AD=EC，DB=AE，
∴ED=AD+AE=EC+DB．