题目内容
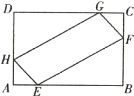
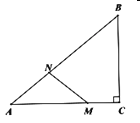
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 以
以![]() 的速度,从点
的速度,从点![]() 运动到点
运动到点![]() ,动点
,动点![]() 同时以
同时以![]() 的速度,从点
的速度,从点![]() 运动到点
运动到点![]() ,当
,当![]() 为直角三角形时,点
为直角三角形时,点![]() 运动的时间为__________
运动的时间为__________![]() .
.
【答案】![]() 或2
或2
【解析】
根据勾股定理求出AB,分∠AMN=90°、∠ANM=90°两种情况,根据相似三角形的性质列出比例式,计算即可.
解:在Rt△ABC中,∠C=90°,
则AB=![]() =
=![]() =5cm,
=5cm,
设点M的运动时间为t秒,
由题意得,CM=t,AN=![]() ,则AM=4t,
,则AM=4t,
当∠AMN=90°时,∠AMN=∠ACB,∠A=∠A,
∴△AMN∽△ACB,
∴![]() ,即
,即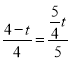 ,
,
解得:t=2,
当∠ANM=90°时,∠ANM=∠ACB,∠A=∠A,
∴△ANM∽△ACB,
∴![]() ,即
,即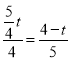 ,
,
解得:t=![]() ,
,
综上所述:当△AMN为直角三角形时,点M的运动秒数为2或![]() ,
,
故答案为:![]() 或2.
或2.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
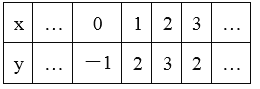
【题目】某数学兴趣小组根据学习函数的经验,对分段函数y=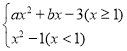 的图象与性质进了探究,请补充完整以下的探索过程.
的图象与性质进了探究,请补充完整以下的探索过程.
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | 0 | ﹣1 | 0 | 1 | 0 | ﹣3 | … |
(1)填空:a= .b= .
(2)①提上述表格补全函数图象;②该函数图象是关于 对称的 (横线上填轴对称或中心对称)图形.
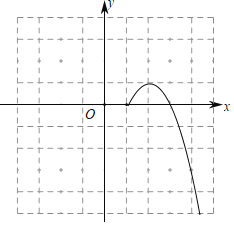
(3)若直线y=![]() x+t与该函数图象有三个交点,直接写出t的取值范围.
x+t与该函数图象有三个交点,直接写出t的取值范围.