题目内容
(1)计算: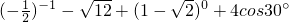
(2)先化简,再求值: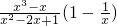 ,其中x=2sin60°-tan45°
,其中x=2sin60°-tan45°
(3)解方程: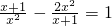 .
.
解:(1)原式=-2-2 +1+4×
+1+4× =-2-2
=-2-2 +1+2
+1+2 =-1;
=-1;
(2)原式= •
• =x+1,
=x+1,
x=2sin60°-tan45°=2× -1=
-1= -1,
-1,
把x的值代入原式得:原式=x+1= -1+1=
-1+1= ;
;
(3)设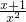 =y,
=y,
则原方程可变形为:y+ =1,
=1,
去分母得:y2-y+2=0,
解得y1=-1,y2=2,
把y的值代入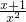 得:①
得:①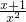 =-1,次方程无解;
=-1,次方程无解;
②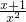 =2,解得:x1=1,x2=-
=2,解得:x1=1,x2=- ;
;
∴原方程的解为:x1=1,x2=- .
.
分析:(1)本题涉及了负整数指数幂、二次根式的化简、零指数幂以及特殊角的三角函数值,计算时针对每个考点依次计算;
(2)先把原式化简,化为最简后,再把x的值代入,注意计算出x的值;
(3)设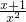 =y,把原方程变形为:y+
=y,把原方程变形为:y+ =1,求出y的值后再代入
=1,求出y的值后再代入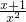 =y即可.
=y即可.
点评:本题考查了分式的化简求值、解分式方程、特殊角的三角函数值、零指数幂、负整数指数幂,此题综合性较强,是中考题中常见的题型.
 +1+4×
+1+4× =-2-2
=-2-2 +1+2
+1+2 =-1;
=-1;(2)原式=
 •
• =x+1,
=x+1,x=2sin60°-tan45°=2×
 -1=
-1= -1,
-1,把x的值代入原式得:原式=x+1=
 -1+1=
-1+1= ;
;(3)设
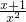 =y,
=y,则原方程可变形为:y+
 =1,
=1,去分母得:y2-y+2=0,
解得y1=-1,y2=2,
把y的值代入
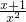 得:①
得:①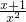 =-1,次方程无解;
=-1,次方程无解;②
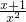 =2,解得:x1=1,x2=-
=2,解得:x1=1,x2=- ;
;∴原方程的解为:x1=1,x2=-
 .
.分析:(1)本题涉及了负整数指数幂、二次根式的化简、零指数幂以及特殊角的三角函数值,计算时针对每个考点依次计算;
(2)先把原式化简,化为最简后,再把x的值代入,注意计算出x的值;
(3)设
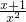 =y,把原方程变形为:y+
=y,把原方程变形为:y+ =1,求出y的值后再代入
=1,求出y的值后再代入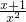 =y即可.
=y即可.点评:本题考查了分式的化简求值、解分式方程、特殊角的三角函数值、零指数幂、负整数指数幂,此题综合性较强,是中考题中常见的题型.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目