题目内容
17.某旅游区一宾馆现有客房120间,每间客房的房价为120元,每天都客满,宾馆装修后,要提高房价.如果一间客房的房价每增加10元,则客房入住数每天就会减少5间,不考虑其他因素,该宾馆的房价提高到多少元时,客房每天的总收入最高?比装修前每天的总收入增加多少元?分析 该宾馆提价后房价为x元/间,则入住的房间有(120-$\frac{x-120}{10}×5$)间,根据总收入=房间单价×入住房间数列出函数关系式,配方可得其最大收入.
解答 解:设该宾馆提价后房价为x元/间,客房总收入为W,根据题意,得
W=x[120-$\frac{x-120}{10}×5$]
=-$\frac{1}{2}$x2+180x
=-$\frac{1}{2}$(x-180)2+16200,
则当x=180时,W取得最大值,最大值为16200元,
比装修前每天的总收入增加16200-120×120=1800(元),
答:该宾馆的房价提高到180元时,客房每天的总收入最高,比装修前每天的总收入增加1800元.
点评 本题主要考查二次函数的实际应用能力,根据题意表示出宾馆入住的房间数量是前提,由相等关系列出函数关系式是关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
7.公共自行车系统建设是今年宁波市政府十个民生实事项目之一,也是缓解城市交通拥堵问题的重要措施.预计年度前投入15000辆公共自行车,用科学记数法表示为( )
| A. | 0.15×105 | B. | 1.5×104 | C. | 1.5×103 | D. | 15×103 |
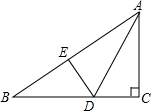 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,将∠C沿AD对折,使点C恰好落在AB边上的点E处,则BD的长度是2$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,将∠C沿AD对折,使点C恰好落在AB边上的点E处,则BD的长度是2$\sqrt{3}$.
