题目内容
在直角坐标系中，△ABC满足，∠C=90°，AC=8，BC=6，点A，B分别在x轴、y轴上，当A点从原点开始在正x轴上运动时，点B随着在正y轴上运动（下图），求原点O到点C的距离OC的最大值，并确定此时图形应满足什么条件．
分析：取斜边AB中点M，连接OM，MC，则△OMC中，两边之和大于第3边，只有O、M、C在一条直线上时候取得最大值，再根据斜边的中线等于斜边的一半，可求解．
解答：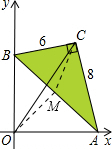
解：取斜边AB中点M，连接OM，MC，则△OMC中，两边之和大于第三边，只有O、M、C在一条直线上时候取得最大值
OM=MC=
AB，AB=
=10．
OC=10，
此时四边形的对角线相等且互相平分，且有一个角是直角，故是矩形．
解：取斜边AB中点M，连接OM，MC，则△OMC中，两边之和大于第三边，只有O、M、C在一条直线上时候取得最大值OM=MC=
| 1 |
| 2 |
| BC2+AC2 |
OC=10，
此时四边形的对角线相等且互相平分，且有一个角是直角，故是矩形．
点评：解决本题的关键是根据题意，找到关键点中点，根据直角三角形斜边的中线是斜边的一半可得解．
练习册系列答案
相关题目
在直角坐标系中，将坐标为（5，6），（1，2），（3，2），（3，0），（7，0），（7，2），（9，2），（5，6）的点用线段依此连接起来形成一个图案．
如图，△ABC在直角坐标系中，