题目内容
 如图,BC是圆O的直径,
如图,BC是圆O的直径, |
| AB |
 |
| AC |
 |
| AC |
考点:圆周角定理,全等三角形的判定与性质
专题:
分析:先根据圆周角定理得出∠BAC=90°,再由
=
得出AB=AC,根据全等三角形的判定定理得出△ABF≌△ACE,由此可得出结论.
 |
| AB |
 |
| AC |
解答:解:CE=BF.
理由:∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠CAE=90°.
∵
=
,
∴AB=AC.
在△ABF与△ACE中,
∵
,
∴△ABF≌△ACE(ASA),
∴CE=BF.
理由:∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠CAE=90°.
∵
 |
| AB |
 |
| AC |
∴AB=AC.
在△ABF与△ACE中,
∵
|
∴△ABF≌△ACE(ASA),
∴CE=BF.
点评:本题考查的是圆周角定理,熟知直径所对的圆周角是直角是解答此题的关键.

练习册系列答案
相关题目

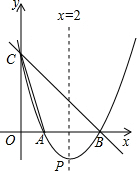 如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴是直线x=2.