题目内容
 如图,已知D为BC上一点,∠B=∠1,∠BAC=74°,则∠2的度数为( )
如图,已知D为BC上一点,∠B=∠1,∠BAC=74°,则∠2的度数为( )| A、37° | B、74° |
| C、84° | D、94° |
考点:三角形的外角性质
专题:
分析:先根据∠B=∠1,∠BAC=74°得出∠BAD+∠B=74°,再由三角形外角的性质即可得出结论.
解答:解:∵∠B=∠1,∠BAC=74°,
∴∠B+∠BAD=∠BAC=74°.
∵∠2是△ABD的外角,
∴∠2=∠B+∠BAD=74°.
故选B.
∴∠B+∠BAD=∠BAC=74°.
∵∠2是△ABD的外角,
∴∠2=∠B+∠BAD=74°.
故选B.
点评:本题考查的是三角形外角的性质,熟知三角形的一个外角等于和它不相邻的两个内角的和是解答此题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
二次函数y=x2-4x+3的图象与x轴的交点坐标是( )
| A、(1,0),(-3,0) |
| B、(1,0),(3,0) |
| C、(-1,0),(-3,0) |
| D、(3,0),(-1,0) |
下列运算中,正确的是( )
| A、a2+a2=a4 |
| B、(a-b)2=a2-b2 |
| C、-a(1-a)=a2-a |
| D、a3•a-4=a-12 |
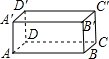 如图是一个放置雕塑的长方形底座,AB=12米,BC=2米,BB′=3米.一只蚂蚁从A点出发,以2厘米/秒的速度沿长方形表面爬到C′至少需要
如图是一个放置雕塑的长方形底座,AB=12米,BC=2米,BB′=3米.一只蚂蚁从A点出发,以2厘米/秒的速度沿长方形表面爬到C′至少需要 如图,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=-2,则m的值为
如图,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=-2,则m的值为
 如图,把面积分别为9与4的两个等边三角形的部分重叠,若两个阴影部分的面积分别记为
如图,把面积分别为9与4的两个等边三角形的部分重叠,若两个阴影部分的面积分别记为