题目内容
如图,已知Rt△ABC≌Rt△DEC,∠E=30°,D为AB的中点,AC=1,若△DEC绕点D顺时针旋转,使ED,CD分别与Rt△ABC的直角边BC相交于M,N.则当△DMN为等边三角形时,AM的值为( )
A.

B.

C.

D.1
【答案】分析:要求AM的长,可以考虑在直角△ACM中利用勾股定理求解,这样就转化为求CM的长.
解答: 解:在Rt△ABC中,∠E=30°,D为AB的中点,
解:在Rt△ABC中,∠E=30°,D为AB的中点,
则△BCD中,BC= ,∠CDB=120°,CD=BD,
,∠CDB=120°,CD=BD,
过点D作DP⊥BC于P点,则PC= ,DP=PC•tan60°=
,DP=PC•tan60°= .
.
在Rt△DMP中,MP=DP•tan30°= ,
,
∴CM=PC-MP= .
.
∵在直角△ACM中,∠CAM=30°.
∴AM=2CM= .
.
故选B.
点评:解决本题的关键是能够正确理解题意,正确作出旋转后的图形,把求线段长的问题转化为三角函数或勾股定理的内容.
解答:
 解:在Rt△ABC中,∠E=30°,D为AB的中点,
解:在Rt△ABC中,∠E=30°,D为AB的中点,则△BCD中,BC=
 ,∠CDB=120°,CD=BD,
,∠CDB=120°,CD=BD,过点D作DP⊥BC于P点,则PC=
 ,DP=PC•tan60°=
,DP=PC•tan60°= .
.在Rt△DMP中,MP=DP•tan30°=
 ,
,∴CM=PC-MP=
 .
.∵在直角△ACM中,∠CAM=30°.
∴AM=2CM=
 .
.故选B.
点评:解决本题的关键是能够正确理解题意,正确作出旋转后的图形,把求线段长的问题转化为三角函数或勾股定理的内容.

练习册系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.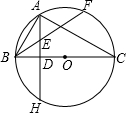 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为