题目内容
【题目】已知直线![]() 和直线
和直线![]()
![]() 不论
不论![]() 为何值,直线
为何值,直线![]() 恒交于一定点
恒交于一定点![]() ,求
,求![]() 点坐标;
点坐标;
![]() 当
当![]() 时,设直线
时,设直线![]() 与
与![]() 轴围成的三角形的面积分别为
轴围成的三角形的面积分别为![]() , 求
, 求![]() .
.
![]() 设直线
设直线![]() 交
交![]() 轴为
轴为![]() 点,交
点,交![]() 轴为
轴为![]() 点,原点为
点,原点为![]() 的面积为
的面积为![]() .
.
求①当![]() 时直线
时直线![]() 的条数各是多少;
的条数各是多少;
②当![]() 且
且![]() 时
时![]() 的函数解析式.
的函数解析式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①见祥解;②
;(3)①见祥解;②![]() .
.
【解析】
(1)把两个解析式联立,解方程组即可;
(2)分别代入![]() ,求出
,求出![]() 值,将其相加即可得出结论;
值,将其相加即可得出结论;
(3)①先用k表示出A点和B点的坐标![]() ,则
,则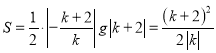 ,然后再当
,然后再当![]() 时讨论即可;
时讨论即可;
②当![]() 且
且![]() ,由①只有一个方程,为
,由①只有一个方程,为![]() ,求解即可.
,求解即可.
![]() 由
由![]() ,得
,得![]() ,则
,则![]()
![]() 设
设![]() 与
与![]() 轴交点横坐标分别是
轴交点横坐标分别是![]() ,则
,则![]() ;
;
![]()
![]()
![]()
当![]() ,
,![]()
![]()
![]()
![]() ①依题意,
①依题意,![]()
则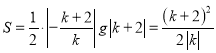
当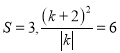 ,即
,即![]() 或
或![]() 解方程,两个方程共有
解方程,两个方程共有![]() 个实数解
个实数解
同理,当![]() ,两个方程共有
,两个方程共有![]() 个实数解
个实数解
当![]() ,两个方程共有
,两个方程共有![]() 个实数解
个实数解
②当![]() 且
且![]() ,由①只有一个方程,为
,由①只有一个方程,为![]() ,则
,则![]()
所以![]()

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩x(分) | 频数(人数) | 频率 |
一 | 50≤x<60 | 2 | 0.04 |
二 | 60≤x<70 | 10 | 0.2 |
三 | 70≤x<80 | 14 | b |
四 | 80≤x<90 | a | 0.32 |
五 | 90≤x<100 | 8 | 0.16 |
请根据表格提供的信息,解答以下问题:

(1)直接写出表中a=________,b=________;
(2)请补全右面相应的频数分布直方图;
(3)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为________.
(4)请根据得到的统计数据,简要分析这些同学的汉字书写能力,并为提高同学们的书写汉字能力提一条建议(所提建议不超过20字).