Question

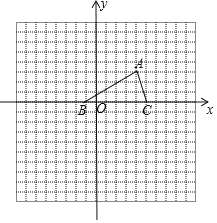
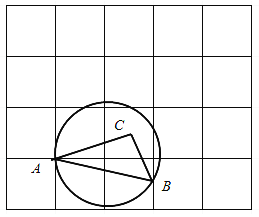
【题目】如图，在每个小正方形的边长为1的网格中，的顶点A在格点上，B是小正方形边的中点，，，经过点A，B的圆的圆心在边AC上．

（Ⅰ）线段AB的长等于_______________；

（Ⅱ）请用无刻度的直尺，在如图所示的网格中，画出一个点P，使其满足，并简要说明点P的位置是如何找到的（不要求证明）_____．

Answer 1

【答案】（Ⅰ）； （Ⅱ）如图，取圆与网格线的交点，连接与相交，得圆心；与网格线相交于点，连接并延长，交于点，连接并延长，与点的连线相交于点，连接，则点满足．

【解析】

（Ⅰ）根据勾股定理即可求出AB的长

（Ⅱ）先确定圆心，根据∠EAF=取格点E、F并连接可得EF为直径，与AC相交即可确定圆心的位置，先在BO上取点P,设点P满足条件，再根据点D为AB的中点，根据垂径定理得出ODAB，再结合已知条件，得出，设PC和DO的延长线相交于点Q，根据ASA可得,可得OA=OQ，从而确定点Q在圆上，所以连接并延长，交于点，连接并延长，与点的连线相交于点，连接即可找到点P

（Ⅰ）解：

故答案为：

（Ⅱ）取圆与网格线的交点，连接，与相交于点O，

∵∠EAF=，∴EF为直径,

∵圆心在边AC上∴点O即为圆心

∵与网格线的交点D是AB中点，连接OD则ODAB，

连接OB，∵,OA=OB

∴∠OAB=∠OBA=，∠DOA=∠DOB=，

在BO上取点P ，并设点P满足条件，∵

∵，

∴∠APO=∠CPO=，

设PC和DO的延长线相交于点Q，则∠DOA=∠DOB=∠POC=∠QOC=

∴∠AOP=∠QOP=，

∵OP=OP, ∴ ∴OA=OQ,

∴点Q在圆上，∴连接并延长，交于点，连接并延长，与点的连线相交于点，连接,则点P即为所求