题目内容
如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-1,0)、B(0,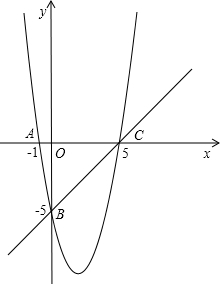 -5)、C(5,0).
-5)、C(5,0).
(1)求此抛物线的表达式;
(2)若平行于x轴的直线与此抛物线交于E、F两点,以线段EF为直径的圆与x轴相切,求该圆的半径;
(3)在点B、点C之间的抛物线上有点D,使△BDC的面积最大,求此时点D的坐标及△BDC的面积.
解:(1)∵抛物线y=ax2+bx+c经过A(-1,0)、
B(0,-5)、C(5,0),代入得:
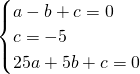 ,
,
解得 ,
,
∴抛物线的表达式为:y=x2-4x-5,
答:此抛物线的表达式是y=x2-4x-5.
(2)如图:
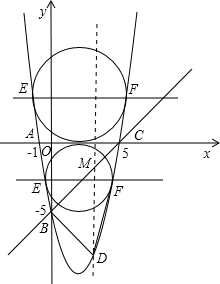 ①当直线EF在x轴上方时,设圆的半径为R(R>0),
①当直线EF在x轴上方时,设圆的半径为R(R>0),
因为抛物线的对称轴为直线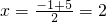
∴F为(R+2,R),
代入抛物线的表达式,得:
R=(R+2)2-4(R+2)-5,
解得: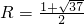 (
(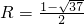 舍去);
舍去);
②当直线EF在x轴下方时,设圆的半径为r(r>0),
则F为(r+2,-r),
代入抛物线的表达式,得:
-r=(r+2)2-4(r+2)-5,
解得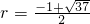 (
(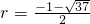 舍去),
舍去),
所以圆的半径为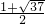 或
或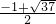 ,
,
答:该圆的半径是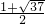 或
或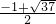 .
.
(3)如图,过D作y轴的平行线,交BC于点M,
设直线BC的表达式是y=kx+b,
把B(0,-5)、C(5,0)代入得: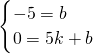 ,
,
解得: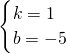
∴直线BC的表达式为:y=x-5,
设D(x,x2-4x-5),则M(x,x-5)
∴DM=(x-5)-(x2-4x-5),
=-x2+5x
=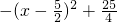
当 时,DM有最大值为
时,DM有最大值为 ,
,
即当D( ,
, )时,△BDC的面积最大=
)时,△BDC的面积最大=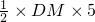
=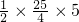
=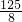 ,
,
答:此时点D的坐标是( ,-
,-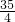 ),△BDC的面积是
),△BDC的面积是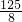 .
.
分析:(1)把A、B、C的坐标代入解析式,得到三元一次方程组,求出方程组的解,即可得到答案;
(2)①当直线EF在x轴上方时,设圆的半径为R(R>0),根据抛物线的对称轴得到F的坐标为(R+2,R),代入抛物线的解析式即可求出半径R;②当直线EF在x轴下方时,设圆的半径为r(r>0),则F为(r+2,-r),与①解法类似即可求出此时的半径r;
(3)过D作y轴的平行线,交BC于点M,设直线BC的表达式是y=kx+b,把B(0,-5)、C(5,0)代入得到方程组,解方程组即可求出直线BC的解析式,设D(x,x2-4x-5),则M(x,x-5),求出DM=-x2+5x,化成顶点式即可求出最大值,即得到△BDC的面积最大值.
点评:本题主要考查了用待定系数法求一次函数、二次函数的解析式,解三元一次方程组、二元一次方程组,二次函数的最值,三角形的面积等知识点,熟练地运用这些知识进行计算是解此题的关键,此题是一个综合性很强的题目,有一定的难度,但题型较好.用的数学思想是分类讨论思想.
B(0,-5)、C(5,0),代入得:
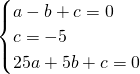 ,
,解得
 ,
,∴抛物线的表达式为:y=x2-4x-5,
答:此抛物线的表达式是y=x2-4x-5.
(2)如图:
 ①当直线EF在x轴上方时,设圆的半径为R(R>0),
①当直线EF在x轴上方时,设圆的半径为R(R>0),因为抛物线的对称轴为直线
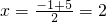
∴F为(R+2,R),
代入抛物线的表达式,得:
R=(R+2)2-4(R+2)-5,
解得:
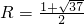 (
(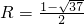 舍去);
舍去);②当直线EF在x轴下方时,设圆的半径为r(r>0),
则F为(r+2,-r),
代入抛物线的表达式,得:
-r=(r+2)2-4(r+2)-5,
解得
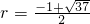 (
(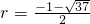 舍去),
舍去),所以圆的半径为
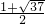 或
或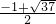 ,
,答:该圆的半径是
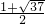 或
或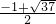 .
.(3)如图,过D作y轴的平行线,交BC于点M,
设直线BC的表达式是y=kx+b,
把B(0,-5)、C(5,0)代入得:
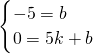 ,
,解得:
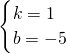
∴直线BC的表达式为:y=x-5,
设D(x,x2-4x-5),则M(x,x-5)
∴DM=(x-5)-(x2-4x-5),
=-x2+5x
=
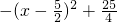
当
 时,DM有最大值为
时,DM有最大值为 ,
,即当D(
 ,
, )时,△BDC的面积最大=
)时,△BDC的面积最大=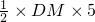
=
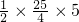
=
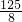 ,
,答:此时点D的坐标是(
 ,-
,-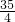 ),△BDC的面积是
),△BDC的面积是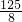 .
.分析:(1)把A、B、C的坐标代入解析式,得到三元一次方程组,求出方程组的解,即可得到答案;
(2)①当直线EF在x轴上方时,设圆的半径为R(R>0),根据抛物线的对称轴得到F的坐标为(R+2,R),代入抛物线的解析式即可求出半径R;②当直线EF在x轴下方时,设圆的半径为r(r>0),则F为(r+2,-r),与①解法类似即可求出此时的半径r;
(3)过D作y轴的平行线,交BC于点M,设直线BC的表达式是y=kx+b,把B(0,-5)、C(5,0)代入得到方程组,解方程组即可求出直线BC的解析式,设D(x,x2-4x-5),则M(x,x-5),求出DM=-x2+5x,化成顶点式即可求出最大值,即得到△BDC的面积最大值.
点评:本题主要考查了用待定系数法求一次函数、二次函数的解析式,解三元一次方程组、二元一次方程组,二次函数的最值,三角形的面积等知识点,熟练地运用这些知识进行计算是解此题的关键,此题是一个综合性很强的题目,有一定的难度,但题型较好.用的数学思想是分类讨论思想.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式. 5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )
5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )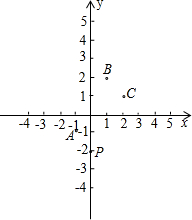 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去. 如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为
如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为 BE.
BE.