Question

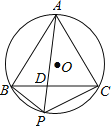
【题目】如图，等腰Rt△ABC的直角顶点B在y轴上，边AB交x轴于点D(，0)，点C的坐标为(﹣4，0)，反比例函数y＝(k≠0)的图象过点A，则k＝_____．

Answer 1

【答案】3

【解析】

过点A作AE⊥y轴于E，根据ABC＝90°，再根据同角的余角相等求出∴∠OCB＝∠ABO，然后通过证得△BOD∽△COB，求得OB＝3，利用“角角边”证明△ABE≌△CBO，根据全等三角形对应边相等可得BE＝OC＝4，AE＝OB＝3，再求出OE，然后写出点A的坐标，再把点A的坐标代入反比例函数解析式计算即可求出k的值．

解：如图，过点A作AE⊥y轴于E，

∵点C的坐标为(﹣4，0)，点D(，0)，

∴OC＝4，OD＝，

∵∠ABC＝90°，

∴∠ABO+∠CBO＝90°，

∵∠OCB+∠CBO＝90°，

∴∠OCB＝∠ABO，

∵∠COB＝∠BOD＝90°，

∴△BOD∽△COB，

∴，

∴OB2＝OCOD＝4×＝9，

∴OB＝3，

在△ABE和△CBO中，

，

∴△ABE≌△CBO(AAS)，

∴BE＝OC＝4，AE＝OB＝3，

∴OE＝BE﹣OB＝4﹣3＝1，

∴点A的坐标为(3，1)，

∵反比例函数y＝(k≠0)的图象过点A，

∴k＝xy＝3×1＝3．

故答案为3．