题目内容
已知四条直线y=kx+3,y=1,y=-3和x=-1所围成的四边形的面积是8,则k的值为
-4或
| 4 |
| 3 |
-4或
.| 4 |
| 3 |
分析:先画出四条直线y=kx+3,y=1,y=-3和x=-1,则得到A点坐标为(-1,1),B点坐标为(-1,-3),讨论:当k<0时,D点的坐标为(-
,1),则DA=-
+1;C点的坐标为(-
,-3),则CB=-
+1,根据四边形ABCD的面积为8得到
(-
+1-
+1)×4=8,解得k=-4;当k>0时,E点的坐标为(-
,1),则EA=-1+
;F点的坐标为(-
,-3),FB=-1+
,根据四边形ABCD的面积为8得到
(-1+
-1+
)×4=8,解得k=
.
| 2 |
| k |
| 2 |
| k |
| 6 |
| k |
| 6 |
| k |
| 1 |
| 2 |
| 2 |
| k |
| 6 |
| k |
| 2 |
| k |
| 2 |
| k |
| 6 |
| k |
| 6 |
| k |
| 1 |
| 2 |
| 2 |
| k |
| 6 |
| k |
| 4 |
| 3 |
解答:解:如图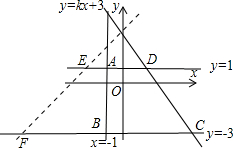 :
:
A点坐标为(-1,1),B点坐标为(-1,-3),
当k<0时,把y=1代入y=kx+3得x=-
,则D点的坐标为(-
,1),所以DA=-
+1,
把y=-3代入y=kx+3得x=-
,则C点的坐标为(-
,-3),所以CB=-
+1,
∵四边形ABCD的面积为8,
∴
(-
+1-
+1)×4=8,解得k=-4;
当k>0时,把y=1代入y=kx+3得x=-
,则E点的坐标为(-
,1),所以EA=-1+
,
把y=-3代入y=kx+3得x=-
,则F点的坐标为(-
,-3),所以FB=-1+
,
∵四边形ABFE的面积为8,
∴
(-1+
-1+
)×4=8,解得k=
;
∴k的值为-4或
.
故答案为:-4或
.
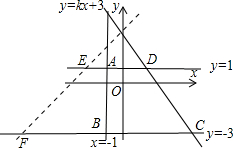 :
:A点坐标为(-1,1),B点坐标为(-1,-3),
当k<0时,把y=1代入y=kx+3得x=-
| 2 |
| k |
| 2 |
| k |
| 2 |
| k |
把y=-3代入y=kx+3得x=-
| 6 |
| k |
| 6 |
| k |
| 6 |
| k |
∵四边形ABCD的面积为8,
∴
| 1 |
| 2 |
| 2 |
| k |
| 6 |
| k |
当k>0时,把y=1代入y=kx+3得x=-
| 2 |
| k |
| 2 |
| k |
| 2 |
| k |
把y=-3代入y=kx+3得x=-
| 6 |
| k |
| 6 |
| k |
| 6 |
| k |
∵四边形ABFE的面积为8,
∴
| 1 |
| 2 |
| 2 |
| k |
| 6 |
| k |
| 4 |
| 3 |
∴k的值为-4或
| 4 |
| 3 |
故答案为:-4或
| 4 |
| 3 |
点评:本题考查了一次函数图象上点的坐标特征:一次函数图象上点的坐标满足y=kx+b(k、b为常数,k≠0).也考查了梯形的面积公式.

练习册系列答案
相关题目
已知四条直线y=kx-3,y=-1,y=3和x=1所围成的四边形的面积是12,则k的值为( )
| A、1或-2 | B、2或-1 | C、3 | D、4 |