Question

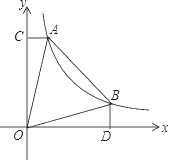
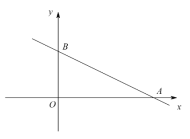
【题目】已知：如图，在平面直角坐标系中，直线与轴相交于点，与轴交于点．抛物线经过点和点，并与轴相交于另一点，对称轴与轴相交于点．

（1）求抛物线的表达式；

（2）求证：；

（3）如果点在线段上，且，求点的坐标．

Answer 1

【答案】（1）；（2）见解析；（3）P(，)

【解析】

（1）利用一次函数，先用含有b的式子表示出A、B两点的坐标，然后代入二次函数可求得b和a的值；

（2）利用两个三角形夹角相等，且夹边成比例证明；

（3）先利用△BCP∽△BAC得到BP的长，再利用△BOA∽△BHP得到点P的横坐标，同理得到纵坐标.

（1）∵一次函数为与轴相交于点，与轴交于点

∴A(－2b，0)，B(0，－b)

将点B代入抛物线得：－b=4，解得：b=－4

∴A(8，0)，B(0，4)

将点A代入抛物线得：0=64a－32a+4，解得：a=

∴抛物线解析式为：

（2）∵抛物线为

∴对称轴为：x=

∴D(2，0)，图形如下：

根据坐标关系得：OD=2，OA=8，OB=4

∵∠BOD=∠BOA

又∵

∴

（3）图形如下，连接CP：

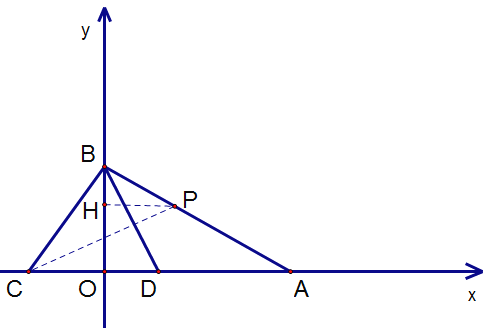
∵△BOD∽△AOB

设∠OBD=∠BAO=a，则∠BCP=∠DBO=a

∴∠BCP=∠BAO=a

∵∠CBP=∠CBA

∴△BCP∽△BAC

∴

∵B(0，4)，C(－4，0)，A(8，0)

∴根据勾股定理：BC=4，AB=4

∴BP=

过点P作x轴的平行线交y轴于点H

∵PH∥x轴

∴，解得：PH=，即点P的横坐标为

同理可得点P的纵坐标为

∴P(，)