ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШбиБп
ГіЗЂЃЌвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШбиБп![]() дЫЖЏЃЌЕНЕу
дЫЖЏЃЌЕНЕу![]() ЭЃжЙЃЌЙ§Еу
ЭЃжЙЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌАб
ЃЌАб![]() ШЦЕу
ШЦЕу![]() ФцЪБеыЗНЯђа§зЊЕУЕН
ФцЪБеыЗНЯђа§зЊЕУЕН ![]() ЃЌЕу
ЃЌЕу![]() ТфдкЯпЖЮ
ТфдкЯпЖЮ![]() ЩЯЃЌЩшЕу
ЩЯЃЌЩшЕу![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ![]() (Уы)
(Уы)
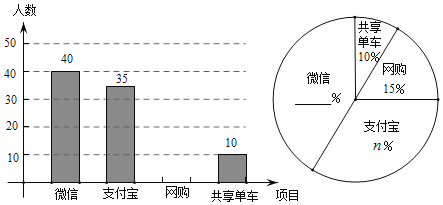
(1)Чѓ![]() ЕФГЄЃЌ(гУКЌ
ЕФГЄЃЌ(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)
ЕФДњЪ§ЪНБэЪО)
(2)ЧѓЕу![]() дк
дк![]() ЕФЦНЗжЯпЩЯЪБ
ЕФЦНЗжЯпЩЯЪБ![]() ЕФГЄ
ЕФГЄ
(3)Щш![]() гы
гы![]() жиКЯВПЗжЭМаЮЕФжмГЄЮЊ
жиКЯВПЗжЭМаЮЕФжмГЄЮЊ![]() ЃЌЕБЕу
ЃЌЕБЕу![]() гыЕу
гыЕу![]() ЁЂ
ЁЂ![]() ОљВЛжиКЯЪБЃЌЧѓ
ОљВЛжиКЯЪБЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕ
жЎМфЕФКЏЪ§ЙиЯЕ
(4)дкЕу![]() дЫЖЏЕФЭЌЪБЃЌЕу
дЫЖЏЕФЭЌЪБЃЌЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы9ИіЕЅЮЛГЄЖШЕФЫйЖШбиелЯп
ГіЗЂЃЌвдУПУы9ИіЕЅЮЛГЄЖШЕФЫйЖШбиелЯп![]() дЫЖЏЃЌЕБЕу
дЫЖЏЃЌЕБЕу![]() ЭЃжЙдЫЖЏЪБЃЌЕу
ЭЃжЙдЫЖЏЪБЃЌЕу![]() вВЫцжЎЭЃжЙЃЌжБНгаДГіЕу
вВЫцжЎЭЃжЙЃЌжБНгаДГіЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЪБ
ЩЯЪБ![]() ЕФжЕ.
ЕФжЕ.
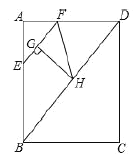
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ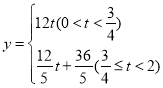 ЃЈ4ЃЉ
ЃЈ4ЃЉ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌЭЦГі
ЃЌЭЦГі![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЎ
ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌзї![]() гк
гк![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гк
гк![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎИљОн
ЃЎИљОн![]() СаГіЗНГЬМДПЩНтОіЮЪЬт
СаГіЗНГЬМДПЩНтОіЮЪЬт
ЃЈ3ЃЉЗжСНжжЧщаЮЗжБ№ЬжТлМДПЩЃКЂйЕБ![]() ЪБЃЌжиЕўВПЗжЪЧ
ЪБЃЌжиЕўВПЗжЪЧ![]() ЃЛЂкЕБ
ЃЛЂкЕБ![]() ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮ
ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮ![]() ЃЎ
ЃЎ
ЃЈ4ЃЉЗжСНжжЧщаЮЗжБ№СаГіЗНГЬМДПЩНтОіЮЪЬтЃЎ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌ
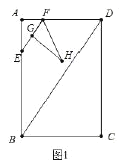
дк![]() жаЃЌЁп
жаЃЌЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() .
.
ЃЈ2ЃЉШчЭМ2жаЃЌзї![]() гк
гк![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гк
гк![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.
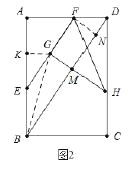
гЩ![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЪБЃЌЕу
ЪБЃЌЕу![]() дк
дк![]() ЕФЦНЗжЯпЩЯ.
ЕФЦНЗжЯпЩЯ.
ЃЈ3ЃЉЂйШчЭМ3 жаЃЌзї![]() гк
гк![]() ЃЌНЛ
ЃЌНЛ![]() гк
гк![]() ЃЎ
ЃЎ
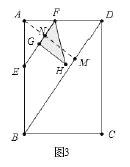
взжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЕБЕу![]() дк
дк![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌжиЕўВПЗжЪЧ
ЪБЃЌжиЕўВПЗжЪЧ![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() .
.
ЂкЕБ![]() ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮ
ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮ![]() .
.
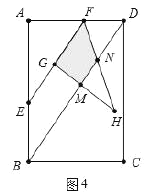
ЫФБпаЮ![]() ЕФжмГЄ
ЕФжмГЄ![]()
![]() .
.
злЩЯЫљЪі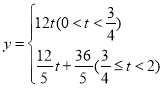
(4)ШчЭМ5жаЃЌзї![]() гк
гк![]() ЃЌЩш
ЃЌЩш![]() НЛ
НЛ![]() гк
гк![]() НЛ
НЛ![]() гк
гк![]() .
.
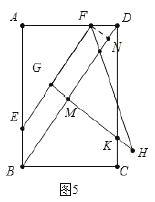
взжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() .
.
гЩЬтвтЕУ![]() Лђ
Лђ![]() .
.
НтЕУ![]() Лђ
Лђ![]() .
.
Ёр![]() Лђ
Лђ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯ.
ЩЯ.

 ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ