题目内容
(本题满分12分)如图,已知直角梯形ABCD ,∠B=900.AD∥BC, 以AB为直径作⊙O,连接OD,并且OD、OC分别平分∠ADC、∠BCD.

(1) 求证:⊙O与CD相切。
(2)若 ,求⊙O的半径?
,求⊙O的半径?
(2)半径为
【解析】
试题分析:(1)过O作OE⊥CD,垂足为E,可以由∠B=900,AD∥BC得到∠A=90°,再由OD平分∠ADC,得出OA=OE,从而的证. (2)由OD、OC分别平分∠ADC、∠BCD和AD∥BC知∠ODE+∠OCE=90°,得到直角三角形,再由三角形的面积的不同求法求得半径.

试题解析:(1)过O作OE⊥CD,垂足为E
∵∠B=900,AD∥BC
∴∠BAD=90°,
∵OD平分∠ADC
∴OA=OE
∴⊙O与CD相切
(2)∵AD∥BC
∴∠ADC+∠BCD=180°
∵OD、OC分别平分∠ADC、∠BCD
∴ ∠ADC+
∠ADC+ ∠BCD=180°
∠BCD=180°
即∠ODE+∠OCE=90°
∴∠COD=90°
根据勾股定理得
又因
解得r=
考点: 切线的判定,角平分线的性质,勾股定理,三角形的面积

练习册系列答案
相关题目
 则它与x轴的另一个交点
则它与x轴的另一个交点 处折断倒下,旗杆顶部落在离旗杆底部12
处折断倒下,旗杆顶部落在离旗杆底部12  处,求出旗杆在折断之前有多高?
处,求出旗杆在折断之前有多高?
 等于( )
等于( ) 是三角形的三边,则
是三角形的三边,则
 中,∠
中,∠ °,所以
°,所以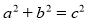
 °,所以
°,所以


