题目内容
已知实数a、b满足条件|a-b|= <1,化简代数式(
<1,化简代数式( -
- )
) ,将结果表示成只含有字母a的形式.
,将结果表示成只含有字母a的形式.
解:∵|a-b|= <1,
<1,
∴a、b同号,且a≠0,b≠0,
∴a-b-1=(a-b)-1<0,
∴( -
- )
) =(
=( -
- )[1-(a-b)]=
)[1-(a-b)]= .
.
①若a、b同为正数,由 <1,得a>b,
<1,得a>b,
∴a-b= ,a2-ab=b,解得b=
,a2-ab=b,解得b= ,
,
∴( -
- )
) =
= =
=
=- •
• =-
=-
=- ;
;
②若a、b同为负数,由 <1,得b>a,
<1,得b>a,
∴a-b=- ,a2-ab=-b,解得b=
,a2-ab=-b,解得b= ,
,
∴(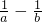 )
) =
= =
=
=
= .
.
综上所述,当a、b同为正数时,原式的结果为- ;当a、b同为负数时,原式的结果为
;当a、b同为负数时,原式的结果为 .
.
分析:由已知可得a-b-1=(a-b)-1<0,据此把代数式化简,又因为要将结果表示成只含有字母a的形式,根据
|a-b|= ,分情况讨论,得出用a表示b的代数式,代入化简即可.
,分情况讨论,得出用a表示b的代数式,代入化简即可.
点评:此题考查二次根式的化简求值,利用了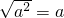 (a≥0)的性质,要充分利用已知条件,难度较大.
(a≥0)的性质,要充分利用已知条件,难度较大.
 <1,
<1,∴a、b同号,且a≠0,b≠0,
∴a-b-1=(a-b)-1<0,
∴(
 -
- )
) =(
=( -
- )[1-(a-b)]=
)[1-(a-b)]= .
.①若a、b同为正数,由
 <1,得a>b,
<1,得a>b,∴a-b=
 ,a2-ab=b,解得b=
,a2-ab=b,解得b= ,
,∴(
 -
- )
) =
= =
=
=-
 •
• =-
=-
=-
 ;
;②若a、b同为负数,由
 <1,得b>a,
<1,得b>a,∴a-b=-
 ,a2-ab=-b,解得b=
,a2-ab=-b,解得b= ,
,∴(
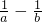 )
) =
= =
=
=

=
 .
.综上所述,当a、b同为正数时,原式的结果为-
 ;当a、b同为负数时,原式的结果为
;当a、b同为负数时,原式的结果为 .
.分析:由已知可得a-b-1=(a-b)-1<0,据此把代数式化简,又因为要将结果表示成只含有字母a的形式,根据
|a-b|=
 ,分情况讨论,得出用a表示b的代数式,代入化简即可.
,分情况讨论,得出用a表示b的代数式,代入化简即可.点评:此题考查二次根式的化简求值,利用了
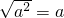 (a≥0)的性质,要充分利用已知条件,难度较大.
(a≥0)的性质,要充分利用已知条件,难度较大. 
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 ,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由. ,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由. ,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.