题目内容
6. 如图,已知A、B两点的坐标分别为(-4,0)、(0,2),⊙C的圆心坐标为(0,-2),半径为2.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是$\frac{44}{3}$.
如图,已知A、B两点的坐标分别为(-4,0)、(0,2),⊙C的圆心坐标为(0,-2),半径为2.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是$\frac{44}{3}$.
分析 当射线AD与⊙C相切时,△ABE面积的最大.设EF=x,由切割线定理表示出DE,可证明△CDE∽△AOE,根据相似三角形的性质可求得x,进而求得BE,然后求得△ABE的面积.
解答 解:当射线AD与⊙C相切时,△ABE面积的最大.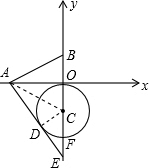
如图,连接AC.
∵A点的坐标为(-4,0),⊙C的圆心坐标为(0,-2),半径为2.
∴AO=4,OC=2,即OC为⊙C的半径,则AO与⊙C相切.
∵AO、AD是⊙C的两条切线,
∴AD=AO=4.
连接CD,设EF=x,
∴DE2=EF•OE,
∵CF=2,
∴DE=$\sqrt{x(4+x)}$.
易证△CDE∽△AOE,则$\frac{CD}{AO}$=$\frac{CE}{AE}$,即$\frac{2}{4}$=$\frac{2+x}{4+\sqrt{x(4+x)}}$,
解得x=$\frac{4}{3}$或x=0(不合题意,舍去),
∴EF=$\frac{4}{3}$,
∴BE=2+4+$\frac{4}{3}$=$\frac{22}{3}$
∴S△ABE=$\frac{1}{2}$BE•OA=$\frac{1}{2}$×$\frac{22}{3}$×4=$\frac{44}{3}$.
故答案为$\frac{44}{3}$.
点评 题是一个动点问题,考查了圆的综合题,解题时,涉及到了切线的性质和三角形面积的计算,解题的关键是确定当射线AD与⊙C相切时,△ABE面积的最大.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
18.运用平方差公式计算(x+2y-1)(x-2y+1),下列变形正确的是( )
| A. | [x-(2y+1)]2 | B. | [x+(2y-1)][x-(2y-1)] | C. | [(x+2y)-1][(x-2y)+1] | D. | [x+(2y+1)]2 |
15.若分式$\frac{6}{a+1}$的值为正整数,则整数a的值有( )
| A. | 3个 | B. | 4个 | C. | 6个 | D. | 8个 |
16.下列解方程错误的是( )
| A. | 由7x=6x-1得7x-6x=-1 | B. | 由5x=10得x=2 | ||
| C. | 由3x=6-x得3x+x=6 | D. | 由$\frac{1}{3}$x=9得x=-3 |
 如图,下面两个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么黄色的对面是绿色.
如图,下面两个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么黄色的对面是绿色. 如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AC边上的一点,且ED⊥FD.
如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AC边上的一点,且ED⊥FD. 根据图中所标注的数据,计算此圆锥的侧面积15πcm2(结果保留π).
根据图中所标注的数据,计算此圆锥的侧面积15πcm2(结果保留π).