题目内容
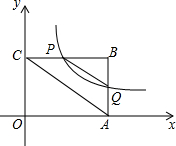 如图,平面直角坐标系中,矩形OABC的一边OA在x轴上且B(4,3).双曲线y=
如图,平面直角坐标系中,矩形OABC的一边OA在x轴上且B(4,3).双曲线y=| k |
| x |
(1)若P为边BC的中点,求双曲线的函数表达式及点Q的坐标;
(2)若双曲线y=
| k |
| x |
(3)连接PQ,AC,当PQ存在时,PQ∥AC是否总成立?若成立请证明,若不成立也请说明理由.
考点:反比例函数综合题
专题:压轴题,数形结合
分析:(1)求反比例函数,找出该曲线上一点的坐标即可;
(2)反比例函数的k=xy,只要知道x和y的值的范围即可得;
(3)求PQ∥AC,即找出线段比值是否相等.
(2)反比例函数的k=xy,只要知道x和y的值的范围即可得;
(3)求PQ∥AC,即找出线段比值是否相等.
解答:解:(1)P为边BC的中点,则P(2,3),k=6,
函数表达式为y=
.
由图可知点Q的横坐标为4,
把x=4代入y=
,解得y=
,
则Q(4,
);
(2)线段BC的纵坐标为3,双曲线y=
(x>0)和线段BC有公共点,即y的值恒为3,
当x值取最大值为4时,可得k最大值为12,
则k取值范围为0<k<12;
(3)成立;点P、Q都是在反比例函数上,
由y=
,可得Q(4,
),P(
,3);
则BP=4-
,BC=4,
BQ=3-
,BA=3;
则
=
=1-
,
=
=1-
;
即
=
,
由平行线分线段成比例定理可得PQ∥AC.
函数表达式为y=
| 6 |
| x |
由图可知点Q的横坐标为4,
把x=4代入y=
| 6 |
| x |
| 3 |
| 2 |
则Q(4,
| 3 |
| 2 |
(2)线段BC的纵坐标为3,双曲线y=
| k |
| x |
当x值取最大值为4时,可得k最大值为12,
则k取值范围为0<k<12;
(3)成立;点P、Q都是在反比例函数上,
由y=
| k |
| x |
| k |
| 4 |
| k |
| 3 |
则BP=4-
| k |
| 3 |
BQ=3-
| k |
| 4 |
则
| PB |
| BC |
4-
| ||
| 4 |
| k |
| 12 |
| BQ |
| BA |
3-
| ||
| 3 |
| k |
| 12 |
即
| PB |
| BC |
| BQ |
| BA |
由平行线分线段成比例定理可得PQ∥AC.
点评:考查反比例函数的性质,以及两直线平行的判定,结合图形解答本题是关键,此题难度不大,属于中档题.

练习册系列答案
相关题目
 如图,若△ABC≌△EBD,且BD=4cm,∠D=60°,则∠ACE=
如图,若△ABC≌△EBD,且BD=4cm,∠D=60°,则∠ACE= 在河湾处M点有一个观察站,观察员要从M点出发,先到AB岸,再到CD岸然后返回M点.画出该船应该走的最短路线(先画图,再用字母表示).
在河湾处M点有一个观察站,观察员要从M点出发,先到AB岸,再到CD岸然后返回M点.画出该船应该走的最短路线(先画图,再用字母表示).