��Ŀ����
15����ͼ1����֪B�������ǣ�6$\sqrt{3}$��6����BA��x����A��BC��y����C��D���߶�OA�ϣ�E��y����������ϣ�DE��BD��M��DE�е㣬��M��OB�ϣ���1����M�������ǣ�2$\sqrt{3}$��2����DE=8��
��2��С�����о���������ʱ���֣����������ֱ����������ഹֱ��ֱ�����������˶������������������߶ε��е㽫��ͬһ��ֱ�����˶���������һ��ʵ����������⣬��ͼ2�����һ����F�ӵ�B������ÿ��1����λ���ȵ��ٶ����A�˶���ͬʱ��һ��G�ӵ�D������ÿ��$\sqrt{3}$����λ���ȵ��ٶ����O�˶�����H�ӵ�E��ʼ��y�����������ɻ�������ʼ�ձ���GH=DE��PΪFG���е㣬QΪGH���е㣬F��G������ֱ��˶��������յ�ʱֹͣ�˶����ֱ�������˶������е�P��Q�˶���·�߳���
��3������PQ�����˶�������ʱ��PQ��С����Сֵ�Ƕ��٣�
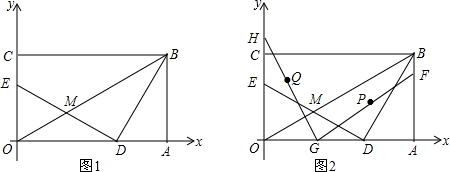
���� ��1���ɵ�B������Ϊ��6$\sqrt{3}$��6��������á�BOA=30�㣬����Rt��EOD�У���ֱ��������б�������ߵ����ʿ�֪��OM=$\frac{1}{2}ED=MD$���Ӷ�����ã���MDO=��BOA=30�㣬Ȼ���֤����EDO=��DBA=30�㣬����������������κ���ֵ�����AD=2$\sqrt{3}$����OD=$\sqrt{3}$��OE=4����ΪM��DE���е㣬���Ե�M������Ϊ��2$\sqrt{3}$��2�����Ӷ������DE=8��
��2���������⻭����P����Q�˶��Ĺ켣����t=0ʱ����P������Ϊ��5$\sqrt{3}$��3������t=4ʱ��P1������Ϊ��3$\sqrt{3}$��1����Ȼ�����������ľ��빫ʽ�����PP1=4����t=6ʱ����Pλ��P2����P1P2=$\frac{1}{2}AF=\frac{1}{2}��2=1$��P���˶���·�߳�PP1+P1P2=5����ΪM��DE���е㣬��EOD=90�㣬����OM=$\frac{1}{2}DE$=4���ʴ˵�M�˶���·��Ϊ��ME��Ȼ����ݻ�����ʽ������õ�M�˶���·�߳���
��3������������λ�ߵ����ʿ�֪��PQ=$\frac{1}{2}$FH�����Ե�FH��y��ʱ��FH��Сֵ=6$\sqrt{3}$������FH�����ʱ�˶�ʱ��Ϊt�룬��AF=6-t��DG=$\sqrt{3}t$���ʴ�OG=��4-t��$\sqrt{3}$����Rt��HOG�У��ɹ��ɶ����ã�OH2=82-3��4-t��2����Ϊ��OH=AF����֪����6-t��2=64-3��4-t��2��Ȼ�ɽ��ʱ��t��ֵ��
��� �⣺�ߵ�B������Ϊ��6$\sqrt{3}$��6����
��tan��BOA=$\frac{AB}{OA}=\frac{6}{6\sqrt{3}}=\frac{\sqrt{3}}{3}$��
���BOA=30�㣮
����Rt��EOD�У���M��ED���е㣬
��OM=$\frac{1}{2}ED=MD$��
���MDO=��BOA=30�㣬
��BD��ED��
���EDB=90�㣮
���EDO+��BDA=90�㣮
�ߡ�BDA+��DBA=90�㣬
���EDO=��DBA=30��
��AD=AB•tan30��=6��$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$��
��OD=6$\sqrt{3}-2\sqrt{3}=4\sqrt{3}$��
��OE=ODtan30��=4$\sqrt{3}$��$\frac{\sqrt{3}}{3}$=4��
��M��DE���е㣬
���M��������2$\sqrt{3}$��2����
��$\frac{OD}{DE}=\frac{\sqrt{3}}{3}$����$\frac{4\sqrt{3}}{DE}=\frac{\sqrt{3}}{2}$��
��DE=8��
��2���������⻭����P����Q�˶��Ĺ켣��
OD=4$\sqrt{3}$����D���˶�ʱ��=$\frac{4\sqrt{3}}{\sqrt{3}}$=4�룻
��F�˶���ʱ��=6��1=6�룻
�ߵ�P��BD���е㣬
���P��������$\frac{4\sqrt{3}+6\sqrt{3}}{2}$��$\frac{0+6}{3}$������P��������5$\sqrt{3}$��3����P1��������3$\sqrt{3}$��1��
��PP1=$\sqrt{��3-1��^{2}+��5\sqrt{3}-3\sqrt{3}��^{2}}$=$\sqrt{16}=4$��
P1P2=$\frac{1}{2}AF=\frac{1}{2}��2=1$
P���˶���·�߳�PP1+P1P2=5��
��M��DE���е㣬��EOD=90��
��OM=$\frac{1}{2}DE$=$\frac{1}{2}��8=4$��
���M�˶���·��Ϊ��ME��
�ߡ�BOA=30�㣬
���EOM=60�㣮
���M�˶���·�߳�=$\frac{60}{360}��2���С�4$=$\frac{4}{3}��$��
��GH=DE��
���G�˶���·�߳�Ϊ��$\frac{4}{3}��$��
��3���ߵ�P��Q�ֱ�ΪFG��GH���е㣬
��PQ=$\frac{1}{2}$FH��
�൱FH��Сʱ��PQ��С��
��FH��y��ʱ��FH��Сֵ=6$\sqrt{3}$��
��ͼ2������FH��
���ʱ�˶�ʱ��Ϊt�룬��AF=6-t��DG=$\sqrt{3}t$
��OG=��4-t��$\sqrt{3}$��
��Rt��HOG�У��ɹ��ɶ����ã�OH2=GH2-OG2
��OH2=82-3��4-t��2��
��OH=AF��
�ࣨ6-t��2=64-3��4-t��2��
��ã�${t}_{1}=\frac{9-\sqrt{61}}{2}$��${t}_{2}=\frac{9+\sqrt{61}}{2}$����ȥ��
�൱�˶�ʱ��Ϊ$\frac{9-\sqrt{61}}{2}$��ʱ��PQ��Сֵ=3$\sqrt{3}$��
���� ������Ҫ��������ı��Ρ������Ρ�������Ǻ�����һԪ���η��̵��ۺ�Ӧ�ã�������P�͵�Q�˶��Ĺ켣�ǽ���Ĺؼ���

 ��ͼ1���ı���ABCD�У�AB��CD��AB=a��CD=b��a��b������E��F�ֱ���AD��BC�ϵĵ㣬��EF��AB����EF��CD��AB�ľ���ֱ�Ϊd1��d2��
��ͼ1���ı���ABCD�У�AB��CD��AB=a��CD=b��a��b������E��F�ֱ���AD��BC�ϵĵ㣬��EF��AB����EF��CD��AB�ľ���ֱ�Ϊd1��d2��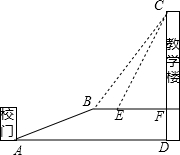 ������һ��������ɽ�£�ij��ѧ��ɽ������У��A������һб��AB������Ϊ13�ף����¶�B������ѧ¥CF��¥��C�����ǡ�CBF=53�㣬��B��4��Զ��E����һ��̨����E������C�����ǡ�CEF=63.4�㣬CF���ӳ��߽�У�Ŵ���ˮƽ����D�㣬FD=5�ף�
������һ��������ɽ�£�ij��ѧ��ɽ������У��A������һб��AB������Ϊ13�ף����¶�B������ѧ¥CF��¥��C�����ǡ�CBF=53�㣬��B��4��Զ��E����һ��̨����E������C�����ǡ�CEF=63.4�㣬CF���ӳ��߽�У�Ŵ���ˮƽ����D�㣬FD=5�ף�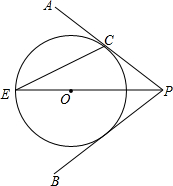 ��ͼ����O�ڡ�APB��ƽ�����ϣ���O��PA�����ڵ�C��
��ͼ����O�ڡ�APB��ƽ�����ϣ���O��PA�����ڵ�C��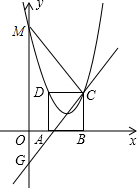 ��ͼ����ƽ��ֱ������ϵxoy�У�����ABCD�ı�AB��x���ϣ���AB=3��BC=2$\sqrt{3}$��ֱ��y=$\sqrt{3}$x-2$\sqrt{3}$������C����y���ڵ�G��
��ͼ����ƽ��ֱ������ϵxoy�У�����ABCD�ı�AB��x���ϣ���AB=3��BC=2$\sqrt{3}$��ֱ��y=$\sqrt{3}$x-2$\sqrt{3}$������C����y���ڵ�G��