题目内容
5.当x=3,y=2时,代数式$\frac{{4xy-4{x^2}-{y^2}}}{2x-y}÷({4{x^2}-{y^2}})$的值是( )| A. | -8 | B. | 8 | C. | $-\frac{1}{8}$ | D. | $\frac{1}{8}$ |
分析 先根据分式混合运算的法则把原式进行化简,再把x=3,y=2代入进行计算即可.
解答 解:原式=$\frac{-(2x-y)^{2}}{2x-y}$•$\frac{1}{(2x-y)(2x+y)}$
=-$\frac{1}{2x+y}$,
当x=3,y=2时,原式=-$\frac{1}{2×3+2}$=-$\frac{1}{8}$.
故选C.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.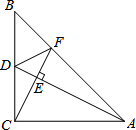 已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )
已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )
 已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )
已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
17.若(a+b)2加上一个单项式后等于(a-b)2,则这个单项式为( )
| A. | 2ab | B. | -2ab | C. | 4ab | D. | -4ab |
15.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
(1)根据表中的数据,分别计算甲、乙两人的平均成绩:$\overline{x_甲}$=9环,$\overline{x_乙}$=9环.
(2)分别计算甲、乙六次测试成绩的方差;S甲2=$\frac{2}{3}$ 环2,S乙2=$\frac{4}{3}$环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
| 甲 | 10 | 9 | 8 | 8 | 10 | 9 |
| 乙 | 10 | 10 | 8 | 10 | 7 | 9 |
(2)分别计算甲、乙六次测试成绩的方差;S甲2=$\frac{2}{3}$ 环2,S乙2=$\frac{4}{3}$环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
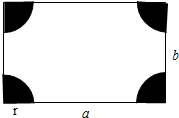 如图,在一长方形休闲广声场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
如图,在一长方形休闲广声场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.